Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số tự nhiên có 6 chữ số đôi một khác nhau có dạng:
Sắp xếp cụm số 3, 4, 5 mà số 4 luôn đứng cạnh 3 và 5 thì ta có 2 cách sắp xếp: 345 và 543.
TH1: Nếu các cụm số 3, 4, 5 đứng đầu có các số tạo thành là: (số)
TH2: Nếu các cụm số 3,4,5 không đứng đầu có 3 cách sắp xếp là: x345xx; xx345x; xxx345.
Khi đó 3 chữ số còn lại có: cách chọn và sắp xếp.
Do đó ta có được các số tạo thành là: (số)
Áp dụng quy tắc cộng có: số thỏa mãn yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
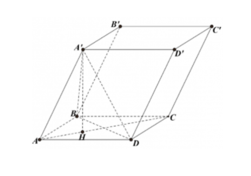
Từ giả thiết ta có các tam giác ABD, là các tam giác đều.
Suy ra ta có: nên H là hình chiếu của A' trên mặt phẳng (ABCD) là tâm đường tròn ngoại tiếp tam giác đều ABD.
Do đó:
Vậy thể tích của khối hộp ABCD.A'B'C'D' là:
Lời giải
Hình chóp có n cạnh bên và n cạnh đáy nên sẽ có 2n cạnh.
Khi đó ta có:
Vậy hình chóp 16 cạnh sẽ có 8 mặt bên và 1 mặt đáy nên tổng số là 9 mặt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Qua ba điểm xác định một và chỉ một mặt phẳng.
B. Qua ba điểm phân biệt xác định một và chỉ một mặt phẳng.
C. Qua ba điểm phân biệt không thẳng hàng xác định một mặt phẳng.
D. Qua ba điểm phân biệt không thẳng hàng xác định một và chỉ một mặt phẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo