Giải bài toán bằng cách lập phương trình hoặc hệ phương trình :

Tìm số tự nhiên có hai chữ số, biết tổng hai chữ số của nó bằng 9, nếu lấy số đó chia cho số viết theo thứ tự ngược lại thì được thương là 2 và còn dư 18 ?

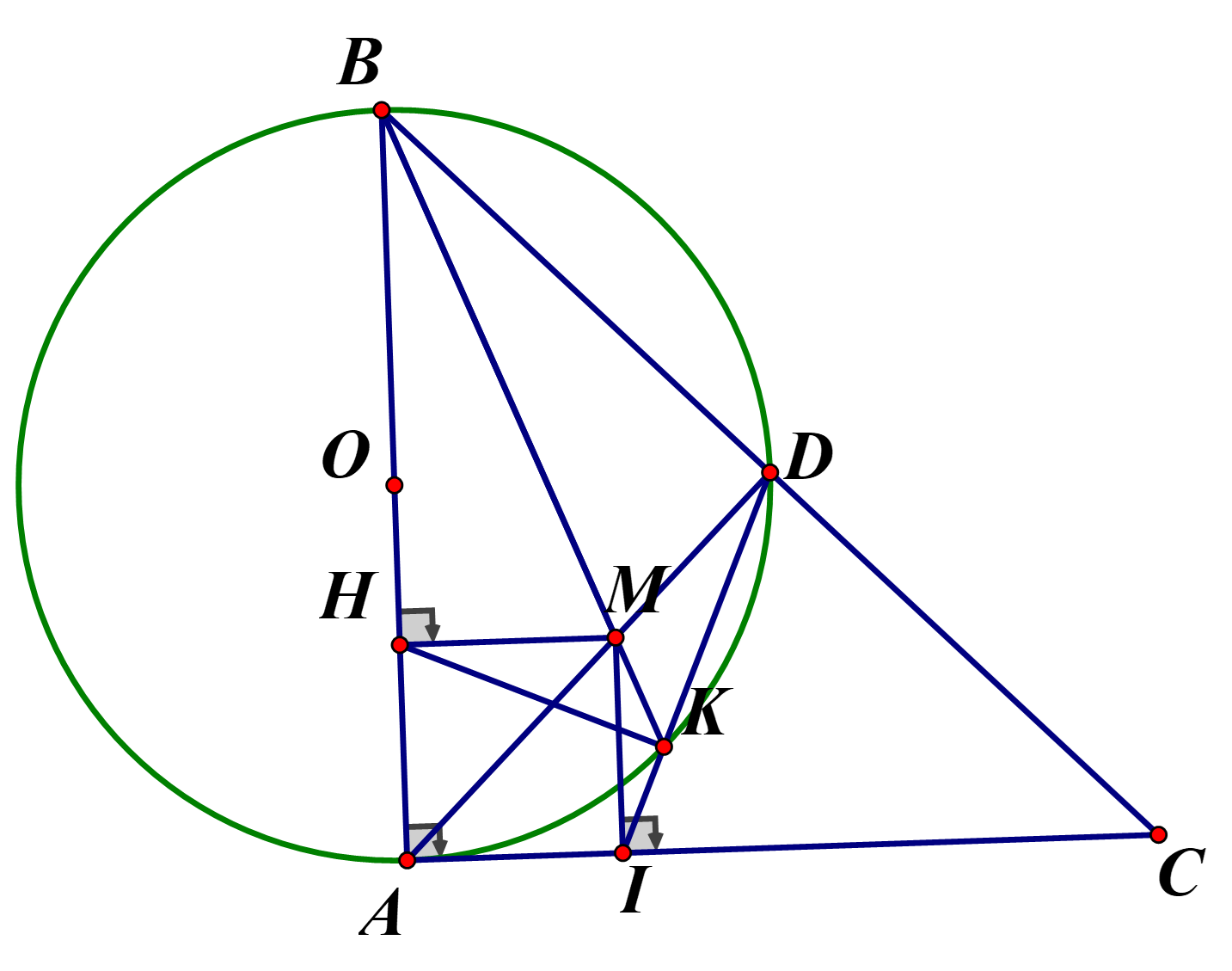
\(a)MI \bot AC,MD \bot BC \Rightarrow \angle MIC + \angle MDC = 90^\circ + 90^\circ = 180^\circ \)

\( \Rightarrow MDCI\)là tứ giác nội tiếp

\(b)MDCI\)là tứ giác nội tiếp \( \Rightarrow \angle MID = \angle MCD\left( 1 \right);\)

\(\Delta ABC\)vuông cân \( \Rightarrow \angle ABD = 45^\circ \Rightarrow \Delta ABD\)cũng vuông cân

\( \Rightarrow \angle BAD = 45^\circ \Rightarrow \angle BAD = \angle DAC = 45^\circ \Rightarrow AD\)là tia phân giác của \(\angle BAC\)

\( \Rightarrow \Delta BAC\)cân tại A, có \(AD\)là phân giác nên đồng thời là trung trực

\( \Rightarrow MB = MC \Rightarrow \angle MBD = \angle MCD\left( 2 \right)\)

\(\left( 1 \right),\left( 2 \right) \Rightarrow \angle MID = \angle MBD = \angle MBC(dfcm)\)

c) \(HK \bot ID \Rightarrow \angle HAI + \angle IKH = 180^\circ \Rightarrow AHKI\)nội tiếp

mà \(AHMI\)cũng nội tiếp (vì \(\angle AHM = 90^\circ = \angle AIM)\)\( \Rightarrow A,H,M,K,I\)cũng thuộc đường tròn

\( \Rightarrow AMKI\)nội tiếp \( \Rightarrow \angle AMK = 90^\circ - \angle HAM = 45^\circ \)

Lại có : \(\angle DIC = \angle DMC = \angle BMD\)(MD là trung trực \(BC)\)

\( \Rightarrow \angle HMA + \angle HMB + \angle AMK = \angle HMB + \angle BMD + \angle HMA = \angle AMD = 180^\circ \)

\( \Rightarrow \angle BMK = 180^\circ \Rightarrow B,M,K\)thẳng hàng

\( = \frac{{{a^3} - {a^2}b - a{b^2} + {b^3}}}{b} = \frac{{{{\left( {a - b} \right)}^2}.\left( {a + b} \right)}}{b} \ge 0\)(vì \(a,b > 0)\)

Vậy \(\frac{{{a^3}}}{b} \ge {a^2} + ab - {b^2}\)

Chứng minh tương tự : \(\frac{{{b^3}}}{c} \ge {b^2} + bc - {c^2} & & & \frac{{{c^3}}}{b} \ge {c^2} + ca - {a^2}\)

\( \Rightarrow \frac{{{a^3}}}{b} + \frac{{{b^3}}}{c} + \frac{{{c^3}}}{a} \ge ab + bc + ca\)

Dấu xảy ra \( \Leftrightarrow a = b = c\)