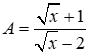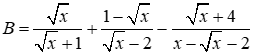Cho a, b, c > 0. Chứng minh :

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Xét hiệu : \(\frac{{{a^3}}}{b} - \left( {{a^2} + ab - {b^2}} \right)\)

\( = \frac{{{a^3} - {a^2}b - a{b^2} + {b^3}}}{b} = \frac{{{{\left( {a - b} \right)}^2}.\left( {a + b} \right)}}{b} \ge 0\)(vì \(a,b > 0)\)

Vậy \(\frac{{{a^3}}}{b} \ge {a^2} + ab - {b^2}\)

Chứng minh tương tự : \(\frac{{{b^3}}}{c} \ge {b^2} + bc - {c^2} & & & \frac{{{c^3}}}{b} \ge {c^2} + ca - {a^2}\)

\( \Rightarrow \frac{{{a^3}}}{b} + \frac{{{b^3}}}{c} + \frac{{{c^3}}}{a} \ge ab + bc + ca\)

Dấu xảy ra \( \Leftrightarrow a = b = c\)

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông cân đỉnh A. Đường tròn đường kính AB cắt BC tại D Điểm M bất kỳ trên đoạn AD kẻ MH, MI lần lượt vuông góc với

1)    Chứng minh: Tứ giác MDCI nội tiếp

2)    Chứng minh:

3)    Kẻ Chứng minh K, M, B thẳng hàng

4)    Khi M di động trên đoạn AD. Chứng minh rằng đường thẳng HK luôn đi qua một điểm cố định

Xem đáp án

Lời giải

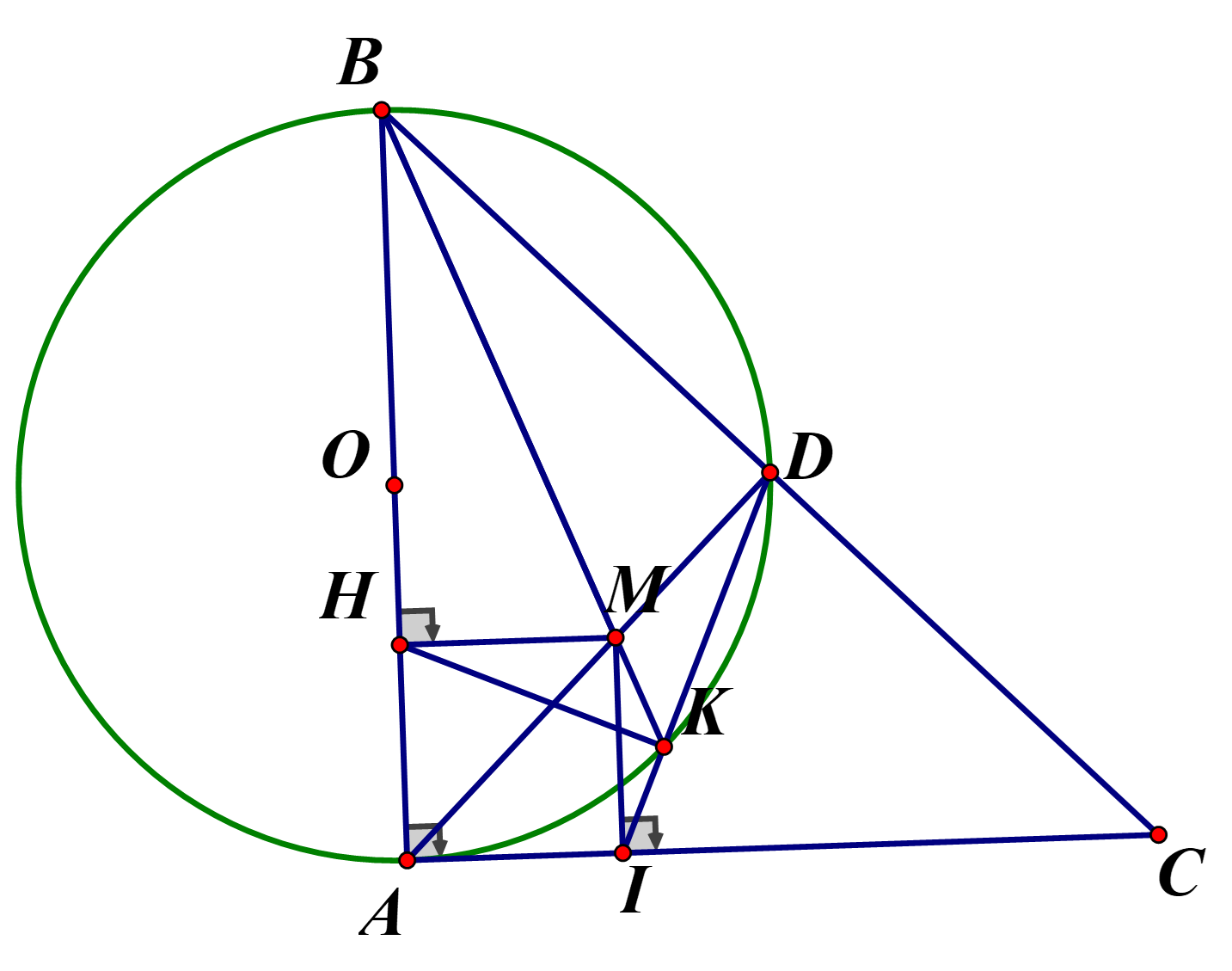
Media VietJack

\(a)MI \bot AC,MD \bot BC \Rightarrow \angle MIC + \angle MDC = 90^\circ + 90^\circ = 180^\circ \)

\( \Rightarrow MDCI\)là tứ giác nội tiếp

\(b)MDCI\)là tứ giác nội tiếp \( \Rightarrow \angle MID = \angle MCD\left( 1 \right);\)

\(\Delta ABC\)vuông cân \( \Rightarrow \angle ABD = 45^\circ \Rightarrow \Delta ABD\)cũng vuông cân

\( \Rightarrow \angle BAD = 45^\circ \Rightarrow \angle BAD = \angle DAC = 45^\circ \Rightarrow AD\)là tia phân giác của \(\angle BAC\)

\( \Rightarrow \Delta BAC\)cân tại A, có \(AD\)là phân giác nên đồng thời là trung trực

\( \Rightarrow MB = MC \Rightarrow \angle MBD = \angle MCD\left( 2 \right)\)

\(\left( 1 \right),\left( 2 \right) \Rightarrow \angle MID = \angle MBD = \angle MBC(dfcm)\)

c) \(HK \bot ID \Rightarrow \angle HAI + \angle IKH = 180^\circ \Rightarrow AHKI\)nội tiếp

mà \(AHMI\)cũng nội tiếp (vì \(\angle AHM = 90^\circ = \angle AIM)\)\( \Rightarrow A,H,M,K,I\)cũng thuộc đường tròn

\( \Rightarrow AMKI\)nội tiếp \( \Rightarrow \angle AMK = 90^\circ - \angle HAM = 45^\circ \)

Lại có : \(\angle DIC = \angle DMC = \angle BMD\)(MD là trung trực \(BC)\)

\( \Rightarrow \angle HMA + \angle HMB + \angle AMK = \angle HMB + \angle BMD + \angle HMA = \angle AMD = 180^\circ \)

\( \Rightarrow \angle BMK = 180^\circ \Rightarrow B,M,K\)thẳng hàng

Câu 2

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình :

Tìm số tự nhiên có hai chữ số, biết tổng hai chữ số của nó bằng 9, nếu lấy số đó chia cho số viết theo thứ tự ngược lại thì được thương là 2 và còn dư 18 ?

Xem đáp án

Lời giải

Gọi \(\overline {ab} \)là số cần tìm \(\left( {a,b \in \mathbb{N}*,a,b \le 9} \right)\). Theo bài ta có hệ phương trình :

\(\left\{ \begin{array}{l}a + b = 9\\\overline {ab} = 2\overline {ba} + 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b = 9\\8a - 19b = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 7\\b = 2\end{array} \right.\)(tm)

Vậy số cần tìm là \(72\)

Câu 3