Câu hỏi:
13/07/2024 835
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)
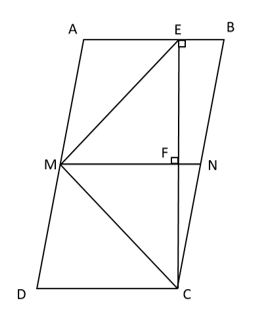
Theo đề ta có: CE vuông góc với AB và CE vuông góc với MN.
Suy ra AB // MN.
Mà ABCD là hình bình hành nên AB // CD.
Do đó MN // DC.
Mặc khác M là trung điểm của AD nên AD = 2MN;
Theo đề AD = 2AB = 2DC (vì ABCD là hình hình hành nên AB = DC).
Do đó MN = DC.
Xét tứ giác MNCD có:
MN // DC (cmt)
MN = DC
Suy ra MNCD là hình bình hành.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng
Xem đáp án »
17/04/2023
30,040
Câu 3:
Cho tam giác ABC có , AC = 2 và . Hỏi bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Cho tam giác ABC có , AC = 2 và . Hỏi bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Xem đáp án »
13/07/2024
14,549
Câu 5:
Cho hình chữ nhật ABCD vẽ tam giá AEC vuông tại E. Chứng minh năm điểm A, B, C, D, cùng thuộc một đường tròn.
Cho hình chữ nhật ABCD vẽ tam giá AEC vuông tại E. Chứng minh năm điểm A, B, C, D, cùng thuộc một đường tròn.
Xem đáp án »
13/07/2024
3,658
Câu 6:
Trong hệ trục tọa độ Oxy cho ba điểm A (1; −4), B (4; 5) và C (0; −9). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng , trong đó a,b là các số nguyên dương a, b < 20. Tính a – b.
Trong hệ trục tọa độ Oxy cho ba điểm A (1; −4), B (4; 5) và C (0; −9). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng , trong đó a,b là các số nguyên dương a, b < 20. Tính a – b.
Xem đáp án »
13/07/2024
3,016
Câu 7:
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng.
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng.
Xem đáp án »
13/07/2024
2,908
về câu hỏi!