Câu hỏi:
12/07/2024 475
Bạn An đã nghĩ ra thuật toán tìm kiếm nhị phân bằng đệ quy theo cách khác như sau:
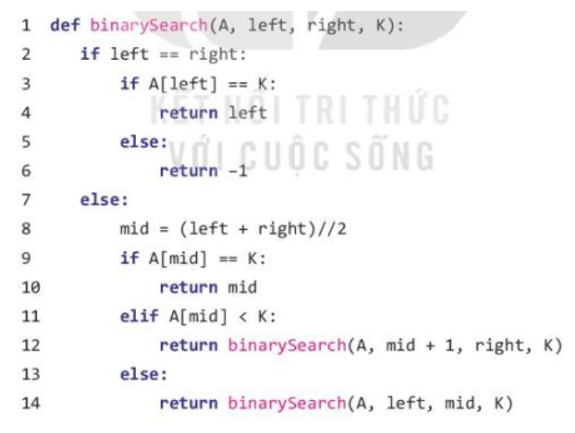
a) Chương trình của bạn An có đúng không?
b) Trong chương trình trên, phần cơ sở là những lệnh nào?
Bạn An đã nghĩ ra thuật toán tìm kiếm nhị phân bằng đệ quy theo cách khác như sau:
a) Chương trình của bạn An có đúng không?
b) Trong chương trình trên, phần cơ sở là những lệnh nào?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Chương trình của An đúng.
b) Phần cơ sở của đoạn lệnh trên là việc kiểm tra điều kiện kết thúc đệ quy, nếu left==right và A[left] == K thì trả về giá trị left, ngược lai nếu A[left] !=K thì trả về -1. Nếu không, tiếp tục tìm kiếm bằng cách tính giá trị mid ở giữa low và high, kiểm tra nó có bằng x hay không, nếu có thì trả về mid, nếu không thì tiếp tục tìm kiếm trong phần bên trái nếu x nhỏ hơn giá trị ở vị trí mid, hoặc phía bên phải nếu x lớn hơn giá trị ở vị trí mid. Quá trình đệ quy này sẽ tiếp tục cho đến khi tìm thấy giá trị x hoặc không tìm thấy và trả về -1.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Không sử dụng đệ quy:
Để tính tổng của một dãy số A, ta có thể sử dụng vòng lặp for để cộng dồn từng phần tử trong dãy A lại với nhau
b) Có sử dụng kĩ thuật đệ quy:
Để tính tổng của một dãy số A sử dụng kĩ thuật đệ quy, ta có thể thực hiện theo thuật toán sau:
1. Kiểm tra điều kiện dừng: nếu A rỗng, tổng của dãy là 0.
2. Trường hợp ngược lại, tính tổng của dãy bằng tổng của phần tử cuối cùng của dãy A (A[-1]) cộng với tổng của dãy A trừ phần tử cuối cùng (A[:-1]).
Lời giải
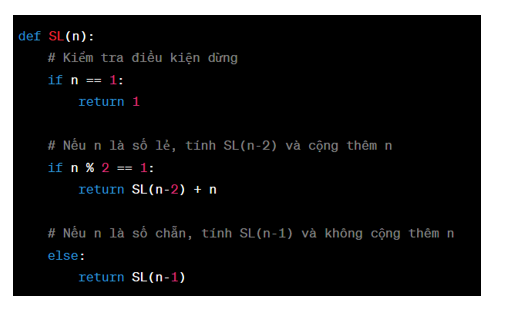
Để tính hàm SL(n) là tổng các số tự nhiên lẻ nhỏ hơn hoặc bằng n theo kĩ thuật đệ quy, ta có thể sử dụng thuật toán sau:
1. Kiểm tra điều kiện dừng: nếu n = 1, trả về giá trị 1.
2. Nếu n là số lẻ, ta tính SL(n-2) và cộng thêm n vào kết quả.
3. Nếu n là số chẵn, ta tính SL(n-1) và không cộng thêm n vào kết quả.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo