Chuyên đề Tin Học 11 KNTT Bài 2. Thiết kế thuật toán đệ quy có đáp án

293 lượt thi 12 câu hỏi

Đề số 1

Đề thi liên quan:

Chuyên đề Tin Học 11 KNTT Bài 1. Đệ quy và hàm đệ quy có đáp án

293 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 3. Thực hành giải toán theo kĩ thuật đệ quy có đáp án

271 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 4. Tháp Hà Nội có đáp án

245 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 5. Thực hành thiết kế thuật toán theo kĩ thuật đệ quy có đáp án

222 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 6. Ý tưởng và kĩ thuật chia để trị có đáp án

273 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 7. Thiết kế thuật toán theo kĩ thuật chia để trị có đáp án

234 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 8. Thực hành thiết thuật toán tìm kiếm theo kĩ thuật chia để trị có đáp án

251 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 9. Sắp xếp trộn có đáp án

222 lượt thi

Chuyên đề Tin Học 11 KNTT Bài 10. Thực hành giải toán bằng kĩ thuật chia để trí có đáp án

220 lượt thi

Danh sách câu hỏi:

Câu 1:

An được giao tìm một thiết kế mới cho bài toán tính tổng S(n) có thể được viết lại như sau: $S (n) = 1 + 2 + 3 + ... + n = 1 + 2 + ... + n - 1 + n = S (n - 1) + n$ . Do đó, việc tính S(n) có thể được tính từ S(n-1), tương tự S(n-1) lại có thể được tính từ S(n-2). Cứ như vậy, cuối cùng sẽ dẫn đến cần tính S(0), nhưng S(0)=0. Em có thể giúp n hoàn thiện ý tưởng trên thành một chương trình hay không?

Xem đáp án

Câu 2:

Trao đổi, thảo luận và tìm hiểu ý tưởng thực hiện các tính toán sau bằng kĩ thuật đệ quy.

1. Tính tổng $S (n) = 1 + 2 + 3 + ... + n$

2. Tính lũy thừa $a^{n} = a \times a \times ... \times a (n l a n)$

3. Tính n giai thừa $n! = 1 \times 2 \times 3 \times ... \times n$

Xem đáp án

Câu 3:

Hãy chỉ ra phần cơ sở và phần đệ quy của các chương trình trên.

Xem đáp án

Câu 4:

Vì sao trong ý tưởng thiết kế đệ quy trên, yêu cầu từ bài toán với kích thước lớn cần phải đưa về cùng bài toán đó với kích thước nhỏ hơn?

Xem đáp án

Câu 5:

Chúng ta đã biết thuật toán tìm kiếm nhị phân trên các dãy phần tử đã sắp xếp. Hãy tìm tới thiết kế mới của thuật toán này theo kĩ thuật đệ quy. Trao đổi, thảo luận và trả lời các câu hỏi sau:

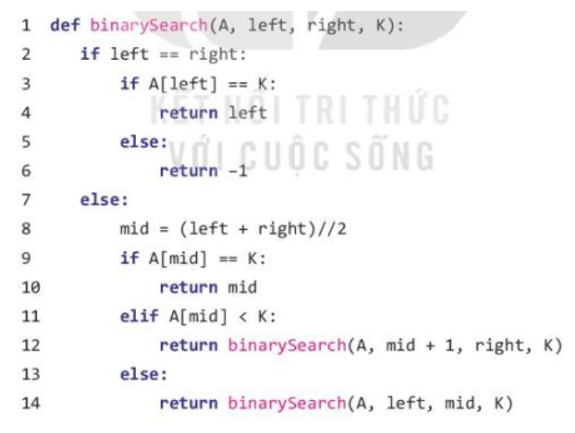
1. Nêu ý tưởng chính của giải thuật tìm kiếm nhị phân sử dụng đệ quy

2. Vị trí nào trong thuật toán có thể gợi ý cho kĩ thuật đệ quy?

3. Phần cơ sở của thiết kế đệ quy nằm ở bước nào?

Xem đáp án

Câu 6:

Trong chương trình trên lệnh nào đóng vai trò là phần cơ sở của đệ quy?

Xem đáp án

Câu 7:

Giả sử A = [1, 3, 7, 9] và K = 10. Nếu áp dụng chương trình trên thì cần mấy lần gọi hàm đệ quy?

Xem đáp án

Câu 8:

Viết chương trình theo kĩ thuật đệ quy để tính hàm SL(n) là tổng các số tự nhiên lẻ nhỏ hơn hoặc bằng n

Xem đáp án

Câu 9:

Cho trước dãy A. Viết chương trình đệ quy để in dãy A theo thứ tự ngược lại.

Xem đáp án

Câu 10:

Viết chương trình tổng $S = 1! + 2! + ... + n!$ theo hai cách:

a) Không sử dụng đệ quy

b) Có sử dụng kĩ thuật đệ quy

Xem đáp án

Câu 11:

Chúng ta đã biết thuật toán sắp xếp chèn trên dãy A cho trước theo hàm sau

Hãy thiết kế lại chương trình trên sử dụng kĩ thuật đệ quy

Xem đáp án

Câu 12:

Bạn An đã nghĩ ra thuật toán tìm kiếm nhị phân bằng đệ quy theo cách khác như sau:

a) Chương trình của bạn An có đúng không?

b) Trong chương trình trên, phần cơ sở là những lệnh nào?

Xem đáp án

4.6

59 Đánh giá

50%

40%

0%

0%

0%

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack