Giải SBT Tin học 11 KNTT Bài 25. Thực hành xác định độ phức tạp thời gian thuật toán có đáp án
30 người thi tuần này 4.6 507 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 4 đề thi giữa kì 1 Tin học 11 Cánh diều có đáp án - Đề 4
Bộ 4 đề thi giữa kì 1 Tin học 11 Cánh diều có đáp án - Đề 3
Bộ 4 đề thi giữa kì 1 Tin học 11 Cánh diều có đáp án - Đề 2
Bộ 4 đề thi giữa kì 1 Tin học 11 Cánh diều có đáp án - Đề 1
Bộ 4 đề thi giữa kì 1 Tin học 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
Bộ 4 đề thi giữa kì 1 Tin học 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 4 đề thi giữa kì 1 Tin học 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 4 đề thi giữa kì 1 Tin học 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Danh sách câu hỏi:
Lời giải
a) T(n) = n + 2log n ≤ 3n với n ≥ 1. Vậy T(n) = O(n).
b) T(n) = n2 + 3nlogn +2n ≤ 6n với n ≥ 1. Vậy T(n) = O(n).
c) T(n) = O(1), độ phức tạp hằng số.
d) T(n) = 2n+1 = 2.2" = O(2").
Lời giải
Hàm trên thực hiện việc tìm phần tử lớn nhất của mảng A.
Gọi n là kích thước của mảng, T(n) là thời gian thực hiện của thuật toán. Thời gian chạy của thuật toán được phân tích như sau:
– Câu lệnh tại dòng 2 cần 1 đơn vị thời gian.
– Vòng lặp for tại dòng 3 biến i chạy từ 1 đến n − 1, nên vòng lặp có n – 1 bước lặp.
– Với mỗi bước lặp chương trình thực hiện 1 lệnh so sánh tại dòng 4 và 1 lệnh gán tại dòng 5 (nếu điều kiện thoả mãn).
– Lệnh trả về tại dòng 6 cần 1 đơn vị thời gian.
Tổng hợp lại chương trình trên có thời gian chạy là
T(n) = 2 + 2(n-1) = 2n = O(n).
Lời giải
Hàm trên thực hiện in ra xâu đảo ngược của xâu đầu vào.
Gọi n là kích thước của xâu đầu vào (số kí tự của xâu), T(n) là thời gian thực hiện
của chương trình. Thời gian chạy của chương trình được phân tích như sau:
– Câu lệnh tại dòng 2 và 3 cần 2 đơn vị thời gian.
– Vòng lặp while thực hiện n lần lặp.
– Với mỗi bước lặp chương trình thực hiện hai lệnh gán tại dòng 5 và 6. – Lệnh trả về tại dòng 7 cần 1 đơn vị thời gian.
Tổng hợp lại chương trình trên có thời gian chạy là T(n) = 2 + 2n+1 = 2n + 3 = O(n).
Lời giải
Gọi n là kích thước của mảng, T(n) là thời gian thực hiện của thuật toán. Thời gian chạy của thuật toán được phân tích như sau:
– Câu lệnh tại dòng 2 cần 1 đơn vị thời gian.
– Vòng lặp for tại dòng 3 biến i chạy từ 1 đến n − 1, nên vòng lặp có n – 1 bước lặp.
– Với mỗi bước lặp chương trình thực hiện:
• Hai lệnh gán tại dòng 4 và 5.
• Vòng lặp while tại dòng 6. Vòng lặp này sẽ chạy tối đa là i lần. Mỗi lần lặp chương trình sẽ thực hiện hai lệnh gán tại dòng 7 và 8, cần 2 đơn vị thời gian. • Lệnh gán tại dòng 9 cần 1 đơn vị thời gian.
Tổng hợp lại chương trình trên có thời gian chạy tối đa là:
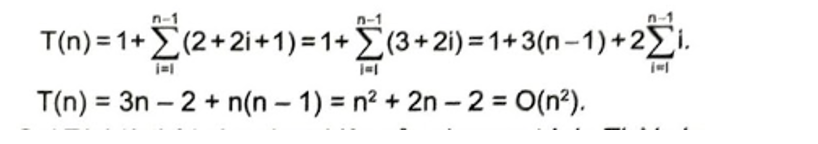
Lời giải
Gọi T(n) là thời gian thực hiện của chương trình. Thời gian chạy của chương trình được phân tích như sau:
– Lệnh gán tại dòng 2 cần 1 đơn vị thời gian.
– Vòng for tại dòng 3, biến i chạy từ 1 đến n, nên vòng lặp có n bước lặp.
– Với mỗi bước lặp trên, chương trình thực hiện
• Vòng lặp tại dòng 4, biến j chạy từ 1 đến i, nên vòng lặp thực hiện i bước lặp. • Với mỗi bước lặp:
a Chương trình thực hiện vòng lặp tại dòng 5, biến k chạy từ j đến j + vòng lặp có i + 1 bước lặp.
a Với mỗi bước lặp chương trình thực hiện 1 lệnh gán tại dòng 6 cần 1 đơn vị thời gian.
– Lệnh trả về tại dòng 7 cần 1 đơn vị thời gian.
Tổng hợp lại, hàm trên có thời gian chạy là
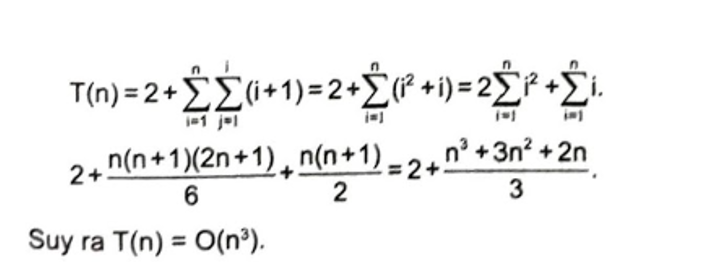
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.



