khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 11
  3. Tin học

Câu hỏi:

11/05/2023 526 Lưu

Trao đổi, thảo luận và tìm hiểu ý tưởng thực hiện các tính toán sau bằng kĩ thuật đệ quy.

1. Tính tổng S(n)=1+2+3+...+n

2. Tính lũy thừa an=a×a×...×a  (n  lan) 

3. Tính n giai thừa n!=1×2×3×...×n

Xem lời giải

Câu hỏi trong đề: Giải SGK Chuyên đề Tin học 11 Bài 2. Thiết kế thuật toán đệ quy !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

1. Tính tổng S(n)=1+2+3+...+n

Bước 1. Bài toán yêu cầu tính tổng của n số nguyên từ 1 đến n. Cần thiết lập hàm S(n) trả về giá trị tổng cần tim.
Bước 2. Điều kiện n ≥ 0.
Với n = 0 ta có S(n) = 0. Đây là phần cơ sở cho điều kiện
dừng của lời gọi đệ quy của hàm S(n).
Bước 3. Dễ thấy S(n) = n + S(n - 1) là công thức truy hồi của hàm S(n) và là cơ sở của lời gọi đệ quy của hàm.Chương trình như sau:

2. Tính lũy thừa an=a×a×...×a  (n  lan) 

Bước 1. Bài toán yêu cầu tính luỹ thừa an. Cần thiết lập hàm exp(a,n) trả về giá trị an.
Bước 2. Điều kiện là n ≥ 0 và theo quy ước thì exp(a,0) = 1 với mọi a. Đây chính là phần cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm exp(a,n).
Bước 3. Ta có an=a · an−1 suy ra exp(a,n) = a × exp(a,n-1), đây là công thức truy hồi tính exp(a,n). Từ đó có thể thiết lập lời gọi đệ quy của hàm này.

3. Tính n giai thừa n!=1×2×3×...×n

Bước 1. Bài toán yêu cầu tính n giai thừa n!. Ta cần thiết lập hàm giaithua(n) trả về giá trị n!.
Bước 2. Điều kiện là n ≥ 0 và quy ước 0! = 1, tức là giaithua (0) = 1. Đây là cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm giaithua(n).
Bước 3. Ta có công thức giaithua(n) = n × giaithua(n-1), đây là công thức truy hồi tính giaithua(n). Từ đó dễ dàng thiết lập lời gọi đệ quy cho hàm này.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Viết chương trình tổng S=1!+2!+...+n! theo hai cách:

a) Không sử dụng đệ quy

b) Có sử dụng kĩ thuật đệ quy

Lời giải

a) Không sử dụng đệ quy:

Để tính tổng của một dãy số A, ta có thể sử dụng vòng lặp for để cộng dồn từng phần tử trong dãy A lại với nhau

Viết chương trình tổng S=1!+2!+...+n! theo hai cách: a) Không sử dụng đệ quy b) Có sử dụng kĩ thuật đệ quy (ảnh 1)

b) Có sử dụng kĩ thuật đệ quy:

Để tính tổng của một dãy số A sử dụng kĩ thuật đệ quy, ta có thể thực hiện theo thuật toán sau:

1. Kiểm tra điều kiện dừng: nếu A rỗng, tổng của dãy là 0.

2. Trường hợp ngược lại, tính tổng của dãy bằng tổng của phần tử cuối cùng của dãy A (A[-1]) cộng với tổng của dãy A trừ phần tử cuối cùng (A[:-1]).

Câu 2

Viết chương trình theo kĩ thuật đệ quy để tính hàm SL(n) là tổng các số tự nhiên lẻ nhỏ hơn hoặc bằng n

Lời giải

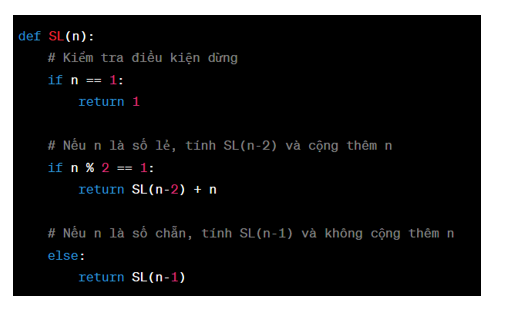
Để tính hàm SL(n) là tổng các số tự nhiên lẻ nhỏ hơn hoặc bằng n theo kĩ thuật đệ quy, ta có thể sử dụng thuật toán sau:

1. Kiểm tra điều kiện dừng: nếu n = 1, trả về giá trị 1.

2. Nếu n là số lẻ, ta tính SL(n-2) và cộng thêm n vào kết quả.

3. Nếu n là số chẵn, ta tính SL(n-1) và không cộng thêm n vào kết quả.

Viết chương trình theo kĩ thuật đệ quy để tính hàm SL(n) là tổng các số tự nhiên lẻ nhỏ hơn hoặc bằng n (ảnh 1)

Câu 3

Cho trước dãy A. Viết chương trình đệ quy để in dãy A theo thứ tự ngược lại.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chúng ta đã biết thuật toán tìm kiếm nhị phân trên các dãy phần tử đã sắp xếp. Hãy tìm tới thiết kế mới của thuật toán này theo kĩ thuật đệ quy. Trao đổi, thảo luận và trả lời các câu hỏi sau:

1. Nêu ý tưởng chính của giải thuật tìm kiếm nhị phân sử dụng đệ quy

2. Vị trí nào trong thuật toán có thể gợi ý cho kĩ thuật đệ quy?

3. Phần cơ sở của thiết kế đệ quy nằm ở bước nào?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Bạn An đã nghĩ ra thuật toán tìm kiếm nhị phân bằng đệ quy theo cách khác như sau:

Bạn An đã nghĩ ra thuật toán tìm kiếm nhị phân bằng đệ quy theo cách khác như sau: (ảnh 1)

a) Chương trình của bạn An có đúng không?

b) Trong chương trình trên, phần cơ sở là những lệnh nào?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Chúng ta đã biết thuật toán sắp xếp chèn trên dãy A cho trước theo hàm sau

Chúng ta đã biết thuật toán sắp xếp chèn trên dãy A cho trước theo hàm sau: (ảnh 1)

Hãy thiết kế lại chương trình trên sử dụng kĩ thuật đệ quy

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Hãy chỉ ra phần cơ sở và phần đệ quy của các chương trình trên.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập