Câu hỏi:
06/06/2023 229Cho một nửa đường tròn đường kính AB. Điểm M chạy trên nửa đường tròn. Kẻ MH vuông góc với AB tại H. Đặt MH = x. Chứng minh rằng:
.
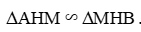
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
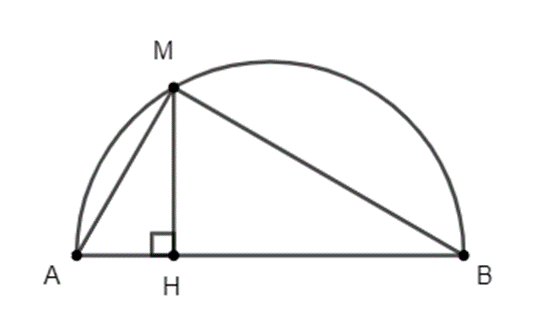
Ta có: ∆AMB nội tiếp trong đường tròn có AB là đường kính nên \(\widehat {AMB} = 90^\circ \)
Suy ra: \(\widehat {MAB} + \widehat {MBA} = 90^\circ \) (1)
∆AMH vuông tại H nên:
\(\widehat {MAH} + \widehat {HMA} = 90^\circ \)
Hay \(\widehat {MAB} + \widehat {HMA} = 90^\circ \) (2)
Từ (1) và (2) suy ra: \(\widehat {MBA} = \widehat {HMA}\)
Xét ∆AHM và ∆MHB có:
\(\widehat {AHM} = \widehat {MHB} = 90^\circ \)
\(\widehat {MBH} = \widehat {HMA}\) (cmt)
Suy ra: (g.g)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số học sinh giỏi, khá, trung bình lần lượt là: a, b, c (học sinh. a, b, c ∈ ℕ*)
Theo bài cho ta có:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{5}\) và b + c – a = 180.
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{5} = \frac{{b + c - a}}{{3 + 5 - 2}} = \frac{{180}}{6} = 30\)
Suy ra:
a = 2.30 = 60 (thỏa mãn điều kiện)
b = 3.30 = 90 (thỏa mãn điều kiện)
c = 5.30 = 150 (thỏa mãn điều kiện)
Vậy số học sinh giỏi, khá, trung bình khối 7 lần lượt là: 60 em; 90 em; 150 em.
Lời giải
Số công nhân sau khi được tăng thêm là:
12 + 8 = 20 (công nhân)
Gọi thời gian 20 công nhân hoàn thành xong công việc là a.
Vì thời gian và số công nhân tỉ lệ nghịch với nhau nên:
5.12 = x.20
\[x = \frac{{5.12}}{{20}} = 3\]
Thời gian hoàn thành công việc được giảm:
5 – 3 = 2 (giờ)
Đáp số: 2 giờ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)