Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
\(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{4}{5}\\\frac{1}{x} - \frac{1}{y} = \frac{1}{5}\end{array} \right.\)
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
\(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{4}{5}\\\frac{1}{x} - \frac{1}{y} = \frac{1}{5}\end{array} \right.\)
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Đặt \(a = \frac{1}{x}\), \(a = \frac{1}{x}\) (điều kiện x ≠ 0; y ≠ 0)
Ta có: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{4}{5}\\\frac{1}{x} - \frac{1}{y} = \frac{1}{5}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = \frac{4}{5}\\a - b = \frac{1}{5}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = \frac{4}{5}\\a = b + \frac{1}{5}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}b + \frac{1}{5} + b = \frac{4}{5}\\a = b + \frac{1}{5}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2b = \frac{3}{5}\\a = b + \frac{1}{5}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}b = \frac{3}{{10}}\\a = b + \frac{1}{5}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}b = \frac{3}{{10}}\\a = \frac{3}{{10}} + \frac{1}{5}\end{array} \right.\)
\[ \Leftrightarrow \left\{ \begin{array}{l}b = \frac{3}{{10}}\\a = \frac{1}{2}\end{array} \right.\]
Khi đó ta được: \(\left\{ \begin{array}{l}\frac{1}{x} = \frac{1}{2}\\\frac{1}{y} = \frac{3}{{10}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \frac{{10}}{3}\end{array} \right.\) (thỏa mãn điều kiện)
Vậy nghiệm của hệ phương trình là: (x; y) = (2; \(\frac{{10}}{3}\))
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để 2 đường thẳng (d) và (d') cắt nhau trên trục tung thì x = 0
Ta có : (d): y = 2m2 + 1
(d'): y = 3.0 + 3 = 3
Vì (d) ∩ (d') nên 2m2 + 1 = 3
Do đó m = 1 hoặc m = − 1.
Lời giải
Ta có sơ đồ:
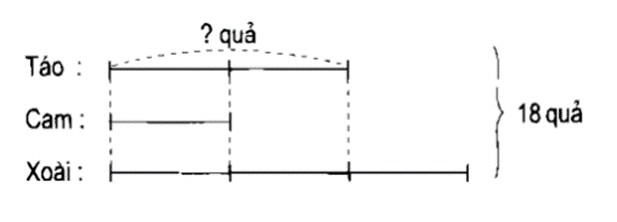
Theo sơ đồ, tổng số phần bằng nhau là:
2 + 1 + 3 = 6 (phần)
Số quả táo là:
18 : 6 × 2 = 6 (quả)
Đáp số: 6 quả
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.