Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chứng mình rằng:

a) \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \);

b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \);

c) \(\overrightarrow {GH} + 2\overrightarrow {GO} = 0\).

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

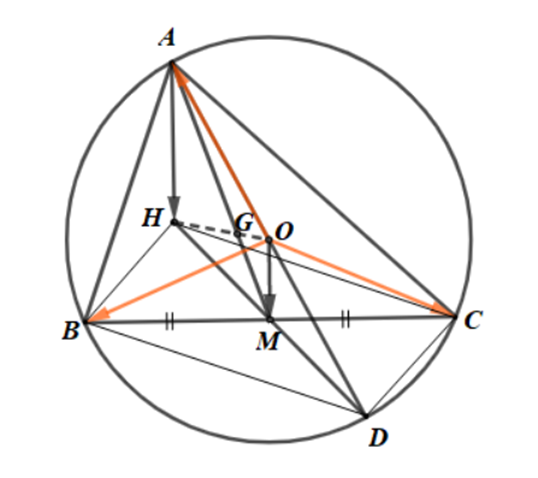
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chứng mình (ảnh 1)

a) Dễ thấy \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \) nếu tam giác ABC vuông.

Nếu tam giác ABC vuông gọi D là điểm đối xứng với A qua O khi đó

BH // DC (cùng vuông góc AC)

BD // CH (cùng vuông góc AB)

Suy ra BDCH là hình bình hành, do đó:

\(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) (1)

Mặt khác vì O là trung điểm AD nên \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} \) (2)

Từ (1) và (2) suy ra \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \)

b) Theo câu a ta có

\(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \Leftrightarrow (\overrightarrow {HO} + \overrightarrow {OA} ) + (\overrightarrow {HO} + \overrightarrow {OB} ) + (\overrightarrow {HO} + \overrightarrow {OC} ) = 2\overrightarrow {HO} \)

⇔ \(\overrightarrow {OA} + \overrightarrow {OA} + \overrightarrow {OA} = \overrightarrow {OH} \) (dpcm)

c) Vì G là trọng tâm tam giác ABC nên \(\overrightarrow {OA} + \overrightarrow {OA} + \overrightarrow {OA} = 3\overrightarrow {OG} \)

Mặt khác theo câu b ta có \(\overrightarrow {OA} + \overrightarrow {OA} + \overrightarrow {OA} = \overrightarrow {OH} \)

Suy ra \(\overrightarrow {OH} = 3\overrightarrow {OG} \Leftrightarrow (\overrightarrow {OG} + \overrightarrow {OH} ) - 3\overrightarrow {OG} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GH} + 2\overrightarrow {GO} = \overrightarrow 0 \)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm m để 2 đường thẳng (d) cắt nhau tại 1 điểm trên trục tung cho hàm số y = (m + 2)x + 2m² + 1 tìm m để hai đường thẳng (d): y = (m + 2)x + 2m² + 1 và (d'): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.

Xem đáp án

Lời giải

Để 2 đường thẳng (d) và (d') cắt nhau trên trục tung thì x = 0

Ta có : (d): y = 2m² + 1

(d'): y = 3.0 + 3 = 3

Vì (d) ∩ (d') nên 2m² + 1 = 3

Do đó m = 1 hoặc m = − 1.

Câu 2

Có tất cả 18 quả táo, cam và xoài. Số quả cam bằng \(\frac{1}{2}\) số quả táo. Số quả xoài gấp 3 lần số quả cam. Tính số quả táo.

Xem đáp án

Lời giải

Ta có sơ đồ:

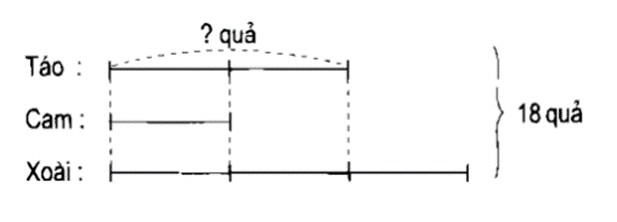
Có tất cả 18 quả táo, cam và xoài. Số quả cam bằng 1/2 số quả táo. Số quả xoài (ảnh 1)

Theo sơ đồ, tổng số phần bằng nhau là:

2 + 1 + 3 = 6 (phần)

Số quả táo là:

18 : 6 × 2 = 6 (quả)

Đáp số: 6 quả

Câu 3