Câu hỏi:
11/07/2024 2,569
Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. Vẽ hình bình hành MANF, gọi O là trung điểm của AF. Chứng minh rằng:
Tứ giác MANF là hình vuông.
Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. Vẽ hình bình hành MANF, gọi O là trung điểm của AF. Chứng minh rằng:
Tứ giác MANF là hình vuông.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
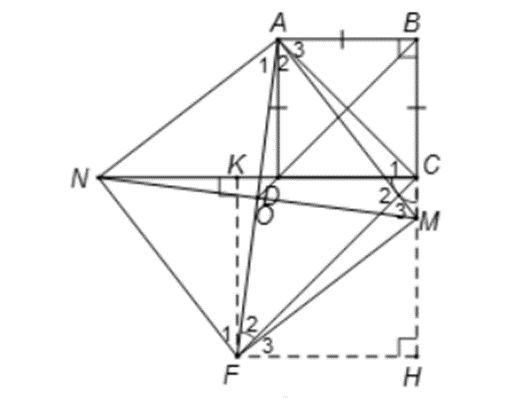
Xét 2 tam giác ABM và ADN ta có:
AB = AD (ABCD là hình vuông)
Và BM = DN (theo đề bài)
Do đó ∆ABM = ∆ADN (c.g.c)
Suy ra AM = AN, \({\widehat A_1} = {\widehat A_3}\) (các cặp cạnh, cặp góc tương ứng).
Hình bình hành MANF có hai cạnh kề bằng nhau nên là hình thoi.
Do góc A2 phụ với góc A3 nên góc A1 phụ với A2 hay \(\widehat {MAN} = 90^\circ \).
Điều này chứng tỏ hình thoi MANF là hình vuông vì có một góc vuông.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để 2 đường thẳng (d) và (d') cắt nhau trên trục tung thì x = 0
Ta có : (d): y = 2m2 + 1
(d'): y = 3.0 + 3 = 3
Vì (d) ∩ (d') nên 2m2 + 1 = 3
Do đó m = 1 hoặc m = − 1.
Lời giải
Ta có sơ đồ:
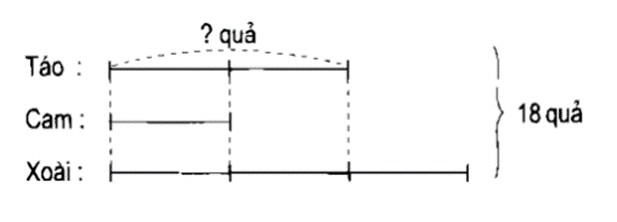
Theo sơ đồ, tổng số phần bằng nhau là:
2 + 1 + 3 = 6 (phần)
Số quả táo là:
18 : 6 × 2 = 6 (quả)
Đáp số: 6 quả
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận