Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC, qua H kẻ một đường thẳng vuông góc với OC cắt (O) tại M (M thuộc cung nhỏ BC), AM cắt (O) tại N (N khác M); gọi K là trung điểm MN.
a) Chứng minh tứ giác ABOC nội tiếp và AB.BM = AM.NB.
b) Chứng minh 5 điểm A, B, K, O, C cùng thuộc một đường tròn và \(\widehat {AMH} = \widehat {AON}\).
c) Kẻ OI vuông góc NB tại I. Chứng minh: I, K, H thẳng hàng.
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC, qua H kẻ một đường thẳng vuông góc với OC cắt (O) tại M (M thuộc cung nhỏ BC), AM cắt (O) tại N (N khác M); gọi K là trung điểm MN.
a) Chứng minh tứ giác ABOC nội tiếp và AB.BM = AM.NB.
b) Chứng minh 5 điểm A, B, K, O, C cùng thuộc một đường tròn và \(\widehat {AMH} = \widehat {AON}\).
c) Kẻ OI vuông góc NB tại I. Chứng minh: I, K, H thẳng hàng.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
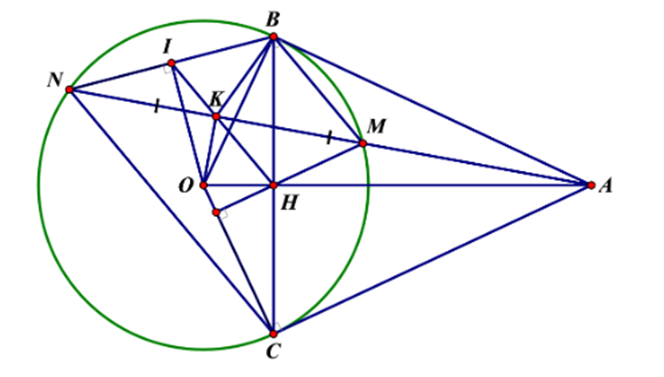
a) Ta có:
• \(\widehat {OBA} = 90^\circ \) (AB là tiếp tuyến của (O))
• \(\widehat {OCA} = 90^\circ \) (AC là tiếp tuyến của (O))
Xét tứ giác ABOC có \(\widehat {OBA} + \widehat {OCA} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra tứ giác ABOC nội tiếp.
Xét ∆ABM và ∆ANB có:
\(\widehat {NAB}\) là góc chung.
\(\widehat {ANB} = \widehat {ABM}\) (Góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung BM).
Suy ra ∆ABM đồng dạng ∆ANB (g.g)
Từ đó suy ra \(\frac{{AM}}{{AB}} = \frac{{BM}}{{NB}} \Leftrightarrow AB.BM = AM.NB\) (đpcm)
b) Tứ giác ABOC nội tiếp có \(\widehat {OBA} = 90^\circ \) suy ra OA là đường kính cũng suy ra tứ giác ABOC nội tiếp đường tròn đường kính OA.
Ta có OK ⊥ MN (tính chất đường kính đi qua trung điểm dây cung thì vuông góc với dây đó).
Suy ra \(\widehat {OKM} = \widehat {OKA} = 90^\circ \) dẫn đến K thuộc đường tròn đường kính OA.
Vậy 5 điểm A, B, C, O, K cùng thuộc 1 đường tròn đường kính OA.
Vì ∆ABM đồng dạng ∆ANB (cmt) nên ta có:
\(\frac{{AB}}{{AN}} = \frac{{AM}}{{AB}}\)
\( \Leftrightarrow \) AB2 = AM.AN
Mà ta cũng có AB2 = AH.AO (∆ABO vuông tại B có đường cao BH).
Suy ra AM . AN = AH . AO
\(\frac{{AM}}{{AO}} = \frac{{AH}}{{AN}}\)
Xét ∆AMH và ∆AON có:
\(\widehat {OAN}\)là góc chung
\(\frac{{AM}}{{AO}} = \frac{{AH}}{{AN}}\) (cmt)
Suy ra ∆AMH đồng dạng ∆AON (c.g.c)
Từ đó suy ra \(\widehat {AMH} = \widehat {AON}\) (hai góc tương ứng).
c) Ta có MH // AC (cùng vuông góc với OC).
Suy ra \(\widehat {KMH} = \widehat {KAC}\) (hai góc đồng vị).
Ta lại có \(\widehat {KBC} = \widehat {KAC}\) (tứ giác KBAC nội tiếp)
Từ đó suy ra \(\widehat {KBH} = \widehat {KMH}\) suy ra tứ giác KBMH nội tiếp.
\(\widehat {MKH} = \widehat {MBH}\) (tứ giác KBMH nội tiếp)
\(\widehat {MNC} = \widehat {MBC}\) (tứ giác NBMC nội tiếp đường tròn (O))
⟹ \(\widehat {MKH} = \widehat {MNC} \Rightarrow KH\,\,{\rm{//}}\,\,NC\) (1)
Ta có H là trung điểm BC (tính chất hai tiếp tuyến cắt nhau).
I là trung điểm NB (đường kính vuông góc với dây cung thì đi qua trung điểm của dây).
Do đó IH là đường trung bình của tam giác NBC hay IH // NC (2)
Từ (1) và (2) suy ra K, H, I thẳng hàng (theo tiên đề Ơ – clit).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để 2 đường thẳng (d) và (d') cắt nhau trên trục tung thì x = 0
Ta có : (d): y = 2m2 + 1
(d'): y = 3.0 + 3 = 3
Vì (d) ∩ (d') nên 2m2 + 1 = 3
Do đó m = 1 hoặc m = − 1.
Lời giải
Ta có sơ đồ:
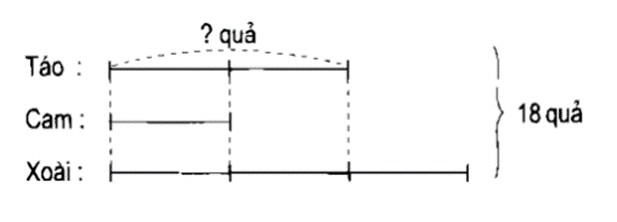
Theo sơ đồ, tổng số phần bằng nhau là:
2 + 1 + 3 = 6 (phần)
Số quả táo là:
18 : 6 × 2 = 6 (quả)
Đáp số: 6 quả
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.