Câu hỏi:
12/07/2024 10,921
Cho các chữ số 1, 3, 4, 7, 8. Từ năm chữ số này có thể lập được tất cả bao nhiêu số chẵn có năm chữ số khác nhau?
Cho các chữ số 1, 3, 4, 7, 8. Từ năm chữ số này có thể lập được tất cả bao nhiêu số chẵn có năm chữ số khác nhau?
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chữ số có năm chữ số cần tìm có dạng: \(\overline {abcde} \)
Vì số cần tìm là số chẵn nên e có 2 cách chọn: 4, 8
Chọn chữ số a có 4 cách chọn
Chọn chữ số b có 3 cách chọn
Chọn chữ số c có 2 cách chọn
Chọn chữ số d có 1 cách chọn
Vậy có tất cả 2.4.3.2.1 = 48 số có thể lập được
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
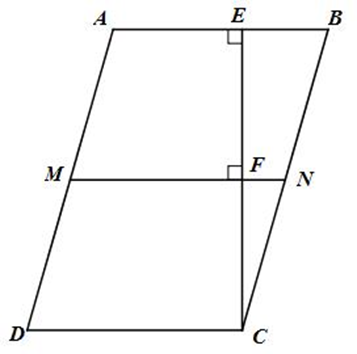
a) Ta có MN ^ CE (gt); AB ^ CE (gt)
Þ MN // AB
Mà AB // CD (ABCD là hình bình hành) nên MN // CD
Tứ giác MNCD có MN // CD
Và MD // CN (AD // BC, M Î AD, N Î BC)
Do đó tứ giác MNCD là hình bình hành.
b) Gọi F là giao điểm của MN và EC
Hình thang AECD (EC // CD) có MF // AE // CD
Và M là trung điểm của AD (gt)
Þ F là trung điểm của EC.
ΔMEC có MF là đường trung tuyến (F là trung điểm của EC)
Và MF là đường cao (MF ^ EC)
Þ ΔMEC cân tại M.
c) Ta có AD = 2AB (gt)
AD = 2MD (M là trung điểm của AD)
Và AB = CD (ABCD là hình bình hành) Þ MD = CD
Hình bình hành MNCD có MD = CD nên là hình thoi.
Þ CM là đường phân giác \(\widehat {EMF} = \widehat {CMF}\)
Mà \(\widehat {EMF} = \widehat {AEM}\) (hai góc so le trong và AE // MF)
Và \(\widehat {CMF} = \widehat {MCD}\) (hai góc so le trong và MF // CD)
Nên \(\widehat {AEM} = \widehat {MCD}\).
Ta có \(\widehat {AEM} = \widehat {MCD};\;2\widehat {MCD} = \widehat {NCD}\) (CM là tia phân giác của \(\widehat {NCD}\))
Và \(\widehat {NCD} = \widehat {BAD}\) (ABCD là hình bình hành)
\( \Rightarrow 2\widehat {AEM} = \widehat {BAD}\).
Lời giải
Quy luật: Lấy 2 số phía trước cộng cho nhau rồi trừ đi 5 sẽ ra số tiếp theo.
Ví dụ:
10 + 13 − 5 = 18
13 + 18 − 5 = 26
………
Vậy số thứ nhất cần điền là:
39 + 60 − 5 = 94
Số thứ hai cần điền là:
60 + 94 − 5 = 149.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)