Cho hình thang ABCD (AB < CD), AD cắt BC tại I, AC cắt BD tại O. Gọi M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cho hình thang ABCD (AB < CD), AD cắt BC tại I, AC cắt BD tại O. Gọi M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng. (ảnh 1)

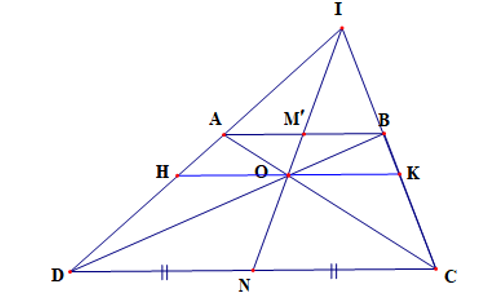
• Gọi M’ là giao điểm của IN và AB. Ta cần chứng minh M’ ≡ M.

Trong DIDN có AM’ // DN nên theo hệ quả định lí Thalès ta có: $\frac{A M^{'}}{D N} = \frac{I M^{'}}{I N}$

Trong DICN có BM’ // CN nên theo hệ quả định lí Thalès ta có: $\frac{B M^{'}}{C N} = \frac{I M^{'}}{I N}$

Suy ra $\frac{A M^{'}}{D N} = \frac{B M^{'}}{C N} (= \frac{I M^{'}}{I N})$

Mà DN = CN nên AM’ = BM’ hay M’ là trung điểm của AB.

Do đó M’ ≡ M nên I, M, N thẳng hàng (*)

• Qua O kẻ đường thẳng song song với CD cắt ID và IC lần lượt tại H và K.

Trong DADC có HO // DC nên theo hệ quả định lí Thalès ta có: $\frac{H O}{D C} = \frac{A O}{A C}$ (1)

Trong DBDC có KO // DC nên theo hệ quả định lí Thalès ta có: $\frac{K O}{D C} = \frac{B O}{B D}$ (2)

Trong DODC có AB // DC nên theo hệ quả định lí Thalès ta có: $\frac{A O}{O C} = \frac{B O}{O D}$

Suy ra $\frac{A O}{A O + O C} = \frac{B O}{B O + O D}$ hay $\frac{A O}{A C} = \frac{B O}{B D}$ (3)

Từ (1), (2) và (3) suy ra $\frac{H O}{D C} = \frac{K O}{D C}$ , do đó HO = KO.

Chứng minh tương tự như trên ta có I, O, N thẳng hàng (**)

Từ (*) và (**) ta có I, M, O, N thẳng hàng.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho (P): y = 2x². Tìm các điểm nằm trên đồ thị (P) có tung độ gấp đôi hoành độ.

Xem đáp án

Lời giải

Giả sử điểm A(x₀; y₀) là điểm thuộc (P) và có tung độ gấp đôi hoành độ.

Suy ra y₀ = 2x₀.

Do điểm thuộc đồ thị (P) nên ta có $y_{0} = 2 x_{0}^{2}$

Khi đó $2 x_{0}^{2} = 2 x_{0}$

$\Leftrightarrow 2 x_{0}^{2} - 2 x_{0} = 0$

$\Leftrightarrow 2 x_{0} (x_{0} - 1) = 0$

$\Leftrightarrow [\begin{array}{l} 2 x_{0} = 0 \\ x_{0} - 1 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x_{0} = 0 \\ x_{0} = 1 \end{array}$

Với x₀ = 0 thì y₀ = 0.

Với x₀ = 1 thì y₀ = 2.

Vậy có 2 điểm thỏa mãn yêu cầu đề bài là (0; 0) và (1; 2).

Câu 2

Tính A = 1 – 2 + 3 – 4 + 5 – 6 + ... + 99 – 100.

Xem đáp án

Lời giải

Biểu thức A có (100 – 1): 1 + 1 = 100 số hạng

Nhóm hai số hạng thành 1 nhóm ra được 100 : 2 = 50 nhóm

A = 1 – 2 + 3 – 4 + 5 – 6 + ... + 99 – 100

A = (1 – 2) + (3 – 4) + (5 – 6) + ... + (99 – 100)

A = (–1) + (–1) + (–1) + ... + (–1)

A = (–1) . 50 = –50

Vậy A = –50.

Câu 3