Câu hỏi:
13/07/2024 389
c) Khi A di động trên đường tròn (O; 3R), gọi M là trực tâm tam giác ABC. Chứng minh M di động trên một đường tròn cố định.
c) Khi A di động trên đường tròn (O; 3R), gọi M là trực tâm tam giác ABC. Chứng minh M di động trên một đường tròn cố định.
Quảng cáo
Trả lời:
Giải bởi Vietjack
c) Ta có: OC ⊥ CA, BM ⊥ CA nên OC // BM.
Tương tự ta có OB // CM.
Xét tứ giác OBMC có OC // BM và OB // CM nên OBMC là hình bình hành.
Lại có OB = OC nên OBMC là hình thoi.
Do đó OM, BC vuông góc với nhau tại trung điểm của mỗi đường, gọi là H.
Khi đó OM = 2OH.
Xét DOBA có đường cao BH, theo hệ thức lượng ta có:
OB2 = OH.OA, suy ra
Do đó .
Vậy khi A di động trên đường tròn (O; 3R) thì M di động trên đường tròn .
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
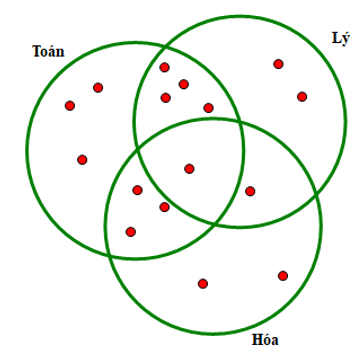
Dựa vào biểu đổ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 5 – 1 = 4 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4 – 1 = 3 (em)
Số học sinh chỉ giỏi Hóa và Lý (không giỏi Toán) là: 2 – 1 = 1 (em)
Số học sinh chỉ giỏi một môn Toán là: 11 – 1 – 4 – 3 = 3 (em)
Số học sinh chỉ giỏi một môn Lý là: 8 – 1 – 4 – 1 = 2 (em)
Mà số học sinh giỏi ít nhất một môn là 16 em
Suy ra số học sinh chỉ giỏi một môn Hóa là: 16 – 4 – 3 – 1 – 3 – 2 – 1 = 2 (em)
Khi đó số học sinh giỏi môn Hóa là: 3 + 1 + 1 + 2 = 7 (em)
Vậy ta chọn đáp án A.
Lời giải
Chiều rộng vườn cây là:
789,25 : 38,5 = 20,5 (m)
Chu vi vườn cây là:
(38,5 + 20,5) × 2 = 118 (m)
Rào xung quanh vườn dài là:
118 – 3,2 = 114,8 (m)
Vậy rào xung quanh vườn dài 114,8 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận