Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Vì ƯCLN(a, b) = 7 nên đặt a = 7k; b = 7q (ƯCLN(q, k) = 1; k < q)
Ta có: a + b = 35
7k + 7q = 35
7(k + q) = 35
k + q = 5
Ta có bảng:
|
k |
1 |
2 |
|
q |
4 |
3 |
|
a |
7 |
14 |
|
b |
28 |
21 |
Vậy các cặp số (a, b) thỏa mãn là {(7; 28); (14; 21)}
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nửa chu vi sân vận động hình chữ nhật là:
400 : 2 = 200 (m)
Ta có sơ đồ:
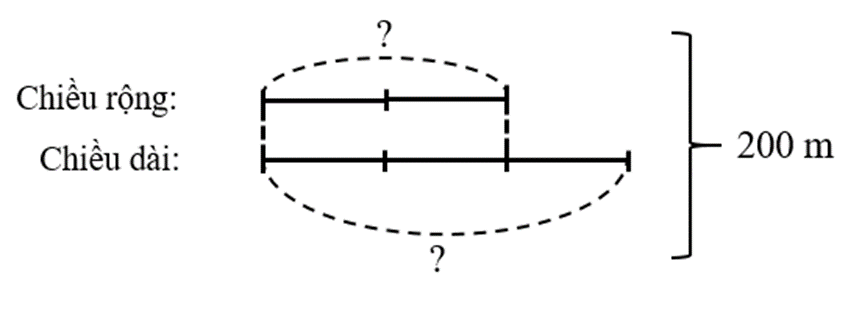
Chiều dài sân vận động hình chữ nhật là:
200 : (2 + 3) × 3 = 120 (m)
Chiều rộng sân vận động hình chữ nhật là:
200 – 120 = 80 (m)
Đáp số: Chiều dài: 120 m;
Chiều rộng: 80 m
Lời giải
Vì khi xếp hàng 3 hoặc hàng 5 đều dư 2 em nên nếu bỏ đi 2 em thì số học sinh lớp 6A chia hết cho cả 3 và 5.
BC(3, 5) = {15, 30, 45,…}
Vì số học sinh lớp 6A từ 40 đến 50 em nên số học sinh lớp 6A là 45 em.
Đáp số: 45 em
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.