Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Gọi S là giao điểm của BC, DE. M là trung điểm của BC. Chứng minh SH2 + AM2 = SM2.
Quảng cáo
Trả lời:
Giải bởi Vietjack
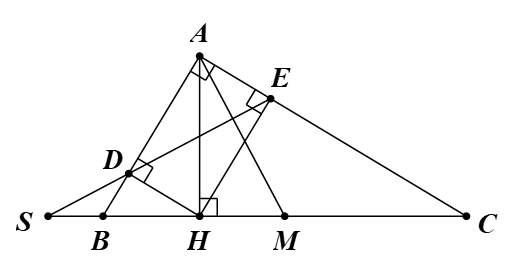
Tam giác ABC vuông tại A có AM là đường trung tuyến.
Suy ra AM = MB = MC.
Tứ giác ADHE, có:
Suy ra tứ giác ADHE là hình chữ nhật.
Xét ∆ADE và ∆EHA, có:
AD = EH (ADHE là hình chữ nhật);
AE chung.
Do đó ∆ADE = ∆EHA (c.g.c).
Suy ra (cặp góc tương ứng).
Mà (đối đỉnh).
Do đó
Vì vậy
Suy ra
Do đó
Xét ∆SHD và ∆SEH, có:
chung;
(chứng minh trên).
Do đó (g.g).
Suy ra
Vì vậy SH2 = SE.SD (1)
Ta có (cùng phụ với ).
Mà (chứng minh trên).
Suy ra
Xét ∆SBD và ∆SEC, có:
chung;
(chứng minh trên).
Do đó (g.g).
Suy ra
Vì vậy SB.SC = SD.SE (2)
Từ (1), (2), suy ra SH2 = SB.SC = (SM – MC)(SM + MC).
= SM2 – MC2 = SM2 – AM2.
Vậy SH2 + AM2 = SM2 (điều phải chứng minh).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gấp rưỡi là gấp 1,5 lần hoặc lần.
Lời giải
Tỉ số phần trăm số học sinh trai và tổng số học sinh của khối lớp 5 là:
100% – 52% = 48%.
Số học sinh trai của khối lớp 5 là:
150 × 48 : 100 = 72 (học sinh).
Đáp số: 72 học sinh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập