Cho 5 số thực không âm a, b, c, d, e có tổng bằng 1. Xếp 5 số này trên một đường tròn. Chứng minh rằng luôn tồn tại một cách xếp sao cho hai số bất kì cạnh nhau có tích không lớn hơn .
Cho 5 số thực không âm a, b, c, d, e có tổng bằng 1. Xếp 5 số này trên một đường tròn. Chứng minh rằng luôn tồn tại một cách xếp sao cho hai số bất kì cạnh nhau có tích không lớn hơn .
Quảng cáo
Trả lời:
Gọi 5 số đó là a; b; c; d; e . ta có a+ b + c + d + e = 1
Không mất tính tổng quát, giả sử 0 < a < b < c < d < e
Nhận xét: c + d < . Vì nếu c + d >
Ta có: 2e > c + d > ⇒ e > ⇒ e + c + d > + = 1 .
Mâu thuẫn với a + b + c + d + e = 1 và a, b, c, d, e không âm.
Áp dụng bất đẳng thức Cô si ta có:
Mặt khác:
1 = a + b + c + d + e > a + 3b + e > 3b + e >
Suy ra:
Ta có: ae < be < ; bc < cd < ; da < dc <
Vậy có thể sắp xếp 5 số a, b, c, d, e theo thứ tự như sau: a, e, b, c, d đều thỏa mãn tích 2 số bất kì cạnh nhau không vượt quá .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi : 1m 20cm = 120 cm.
Diện tích căn phòng đó là :
6 . 4 = 24 (m2) = 240000 (cm2)
Diện tích một mảnh gỗ hình chữ nhật là :
120 . 20 = 2400 (cm2)
Cần số mảnh gỗ để lát kín sàn căn phòng đó là :
240000 : 2400 = 100 (mảnh gỗ)
Đáp số: 100 mảnh gỗ.
Lời giải
Theo đề bài ta có sơ đồ:
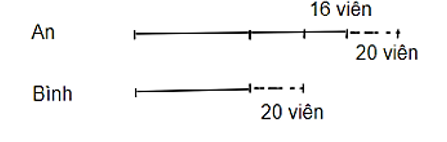
Dựa vào sơ đồ, ta thấy An có nhiều hơn Bình:
20 + 20 + 16 = 56 (viên bi)
Số viên bi An có là:
(120 + 56) : 2 = 88 (viên bi)
Số viên bi Bình có là:
120 – 88 = 32 (viên bi)
Đáp số: An: 88 viên bi
Bình: 32 viên bi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.