Câu hỏi:

13/07/2024 1,873

Cho tam giác ABC có 3 góc nhọn, H là trực tâm, G là trọng tâm. Chứng minh rằng nếu tanB. tanC = 3 thì OH // BC.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

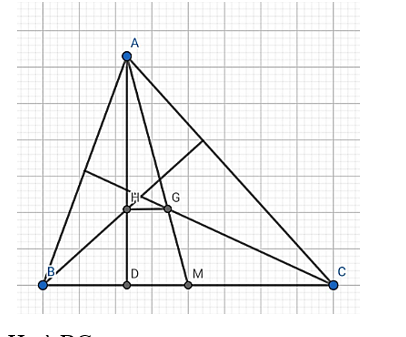
Cho tam giác ABC có 3 góc nhọn, H là trực tâm, G là trọng tâm. Chứng minh rằng nếu tanB. tanC = 3 thì OH // BC. (ảnh 1)

Gọi D là giao điểm của AH và BC

⇒ AD ⊥ BC

M là trung điểm BC nên $\frac{A M}{G M} = 3$ (1)

Xét ΔADC và ΔBDH có:

$\hat{A D C} = \hat{B D H}$ = 90°

$\hat{D A C} = \hat{D B H}$

Do đó ΔADC ᔕ ΔBDH(g.g)

⇒ $\frac{A D}{B D} = \frac{D C}{D H} \Rightarrow \frac{A D}{B D . D C} = \frac{1}{D H}$

⇒ $\frac{A D . A D}{B D . D C} = \frac{A D}{D H}$

⇒ tanB. tanC = $\frac{A D}{D H}$

⇒ $\frac{A D}{D H}$ = 3 (2)

Từ (1) và (2) ⇒ $\frac{A D}{D H}$ = $\frac{A M}{G M}$

⇒ HG // BC (định lý Thales đảo).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

An và Bình có tất cả 120 viên bi. Nếu An cho Bình 20 viên bi thì Bình sẽ có ít hơn An là 16 viên bi. Vậy mỗi bạn An, Bình có bao nhiêu viên bi?

Xem đáp án

Lời giải

Theo đề bài ta có sơ đồ:

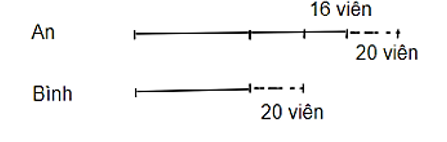
An và Bình có tất cả 120 viên bi. Nếu An cho Bình 20 viên bi thì Bình sẽ có ít hơn An là 16 viên bi. Vậy mỗi bạn An, Bình có bao nhiêu viên bi? (ảnh 1)

Dựa vào sơ đồ, ta thấy An có nhiều hơn Bình:

20 + 20 + 16 = 56 (viên bi)

Số viên bi An có là:

(120 + 56) : 2 = 88 (viên bi)

Số viên bi Bình có là:

120 – 88 = 32 (viên bi)

Đáp số: An: 88 viên bi

Bình: 32 viên bi

Câu 2

Người ta lát sàn một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 4m bằng những mảnh gỗ hình chữ nhật có chiều dài 1m20cm, chiều rộng 20 cm. Hỏi cần bao nhiêu mảnh gỗ để lát kín sàn căn phòng đó?

Xem đáp án

Lời giải

Đổi : 1m 20cm = 120 cm.

Diện tích căn phòng đó là :

6 . 4 = 24 (m²) = 240000 (cm²)

Diện tích một mảnh gỗ hình chữ nhật là :

120 . 20 = 2400 (cm²)

Cần số mảnh gỗ để lát kín sàn căn phòng đó là :

240000 : 2400 = 100 (mảnh gỗ)

Đáp số: 100 mảnh gỗ.

Câu 3