Chứng minh rằng với mọi x, y thuộc ℤ thì A = (x – y)(x – 2y)(x – 3y)(x – 4y) + y4 là số chính phương.

N = (x – y)(x – 2y)(x – 3y)(x – 4y) + y4 N = [(x – y)(x – 4y)][(x – 2y)(x – 3y)] + y4 N = (x2 – 5xy + 4y2)(x2 – 5xy + 6y2) + y4 Đặt x2 – 5xy + 5y2 = a, ta được: N = (a – y2)(a + y2) + y4 N = a2 – y4 + y4 N = a2 N = (x2 – 5xy + 5y2)2 Vậy N là số chính phương.

Câu hỏi:

13/07/2024 3,108

Chứng minh rằng với mọi x, y thuộc ℤ thì

A = (x – y)(x – 2y)(x – 3y)(x – 4y) + y⁴ là số chính phương.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

N = (x – y)(x – 2y)(x – 3y)(x – 4y) + y⁴

N = [(x – y)(x – 4y)][(x – 2y)(x – 3y)] + y⁴

N = (x² – 5xy + 4y²)(x² – 5xy + 6y²) + y⁴

Đặt x² – 5xy + 5y² = a, ta được:

N = (a – y²)(a + y²) + y⁴

N = a² – y⁴ + y⁴

N = a²

N = (x² – 5xy + 5y²)²

Vậy N là số chính phương.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hùng và Dũng có tất cả 46 viên bi. Nếu Hùng cho Dũng 5 viên bi thì số bi của 2 bạn sẽ bằng nhau. Vậy lúc đầu bạn Hùng và Dũng mỗi bạn có bao nhiêu viên bi?

Xem đáp án

Lời giải

Ban đầu Hùng có nhiều hơn Dũng:

5 + 5 = 10 (viên bi).

Số viên bi của bạn Hùng là:

(46 + 10) : 2 = 28 (viên bi).

Số viên bi của bạn Dũng là:

46 – 28 = 18 (viên bi).

Đáp số: Hùng: 28 viên bi; Dũng: 18 viên bi.

Câu 2

Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh:

a) ∆ADM = ∆CBN.

Xem đáp án

Lời giải

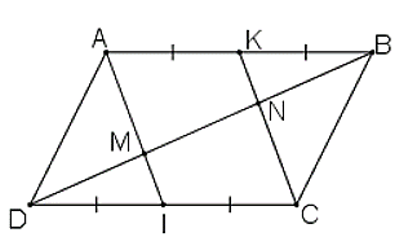
Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: a) ∆ADM = ∆CBN. (ảnh 1)

a) ABCD là hình bình hành

⇒ AB // CD ⇒ AB // IC

AB = CD

Mà K, I lần lượt là trung điểm của AB và CD.

⇒AK = IC

Mà AK // IC

⇒ AKIC là hình bình hành

Xét ΔADI và ΔBCKcó:

DI = BK

AI = CK

AD = BC

⇒ ΔADI = ΔBCK (c.c.c)

⇒ $\hat{D A I} = \hat{B C K}$

Xét ΔADM và ΔCBN có:

$\hat{D A I} = \hat{B C K}$

AD=BC

$\hat{A D B} = \hat{D B C}$ ( Do AD//BC)

⇒ ΔADM = ΔCBN (g.c.g)

Câu 3