Quảng cáo
Trả lời:
Giải bởi Vietjack
n3 (n2 – 7)2 – 36n
= n [n2 (n2 – 7)2 – 62]
= n [n (n2 – 7) – 6][ n (n2 – 7) + 6]
= n (n3 – 7n – 6)(n3 – 7n + 6)
= n (n3 – 3n2 + 3n2 – 9n + 2n – 6)( n3 + 3n2 – 3n2 – 9n + 2n + 6)
= n [(n2 (n – 3) + 3n (n – 3) + 2(n – 3)][(n2 (n + 3) – 3n (n – 3) + 2(n + 3)]
= n(n – 3)(n + 3)(n2 + 3n + 2)(n2 – 3n + 2)
= n(n – 3)(n + 3)(n + 1)(n + 2)(n – 1)(n – 2).
Ta thấy đây là 7 số tự nhiên liên tiếp nên sẽ tồn tại ít nhất 1 số chia hết cho 7.
Suy ra: tích của 7 số tự nhiên liên tiếp chia hết cho 7 hay n3 (n2 – 7)2 – 36n chia hết cho 7.
Vậy n3 (n2 – 7)2 – 36n chia hết cho 7.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số phần trăm vải chỉ may áo là:
100 – 40 = 60 (%)
Số vải may áo là:
545 × 60 : 100 = 327(m)
Đáp số: 327 m.
Lời giải
Bước 1: Xác định tổng
- Tổng các số từ 1 đến 9 là: 1 + 2 +....+ 9 = 45
- Vì 3 ô cộng lại đều bằng nhau nên: Tổng 3 ô là 45 : 3 = 15
Bước 2: Lấy 15 : 3 = 5 suy ra ô trung tâm phải là 5
Bước 3: Chỉ cần nghĩ ra 2 số cộng lại bằng 10 (vì đều cộng với số 5): 10 = 1 + 9 = 2 + 8 = 3 + 7 = 4 + 6
Bước 4: Điền vào các ô theo cặp số.
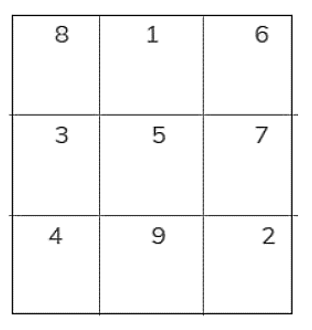
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo