Quảng cáo
Trả lời:
A = 1 + 4 + 42 + … + 42021
A = (1 + 4 + 42) + (43 + 44 + 45) + … + (42019 + 42020 + 42021)
A = (1 + 4 + 42) + 43(1 + 4 + 42) + … + 42019 (1 + 4 + 42)
A = (1 + 4 + 42)(1 + 43 + … + 42019)
A = 21 . (1 + 43 + … + 42019)
Vì 21 chia hết cho 21 nên 21 . (1 + 43 + … + 42019) chia hết cho 21.
Vậy A chia hết cho 21.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
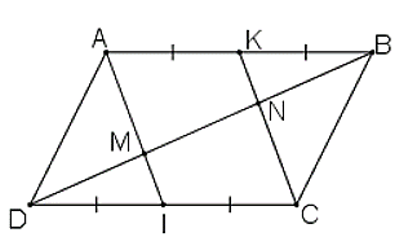
a) ABCD là hình bình hành
⇒ AB // CD ⇒ AB // IC
AB = CD
Mà K, I lần lượt là trung điểm của AB và CD.
⇒AK = IC
Mà AK // IC
⇒ AKIC là hình bình hành
Xét ΔADI và ΔBCKcó:
DI = BK
AI = CK
AD = BC
⇒ ΔADI = ΔBCK (c.c.c)
⇒
Xét ΔADM và ΔCBN có:
AD=BC
( Do AD//BC)
⇒ ΔADM = ΔCBN (g.c.g)Lời giải
Ban đầu Hùng có nhiều hơn Dũng:
5 + 5 = 10 (viên bi).
Số viên bi của bạn Hùng là:
(46 + 10) : 2 = 28 (viên bi).
Số viên bi của bạn Dũng là:
46 – 28 = 18 (viên bi).
Đáp số: Hùng: 28 viên bi; Dũng: 18 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.