Cho tam giác ABC, gọi D là trung điểm của AB, trên tia BC lấy điểm E và F sao cho BE = EF = FC. Trên tia đối của tia BA lấy điểm G sao cho BG = BD. Chứng minh: AF, CD, GE đồng quy.
Cho tam giác ABC, gọi D là trung điểm của AB, trên tia BC lấy điểm E và F sao cho BE = EF = FC. Trên tia đối của tia BA lấy điểm G sao cho BG = BD. Chứng minh: AF, CD, GE đồng quy.
Quảng cáo
Trả lời:
Giải bởi Vietjack
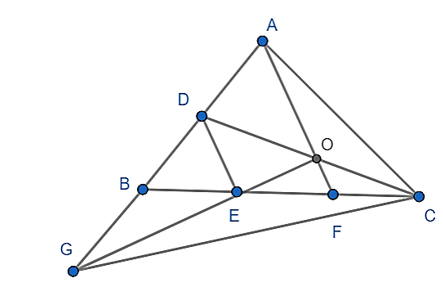
Gọi giao điểm của AF và CD là O.
∆ABF có D, E là trung điểm AB, BF nên DE là đường trung bình của tam giác ABF
⇒ DE // AF hay DE // OF
∆CDE có OF // DE, F là trung điểm CE nên O là trung điểm của CD.
Xét ∆CDG có: CE = CB, CB là đường trung tuyến
Nên E là trọng tâm của ∆CDG
Hay GE đi qua trung điểm CD tức GE đi qua O.
Vậy AF, CD, GE đồng quy tại O.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
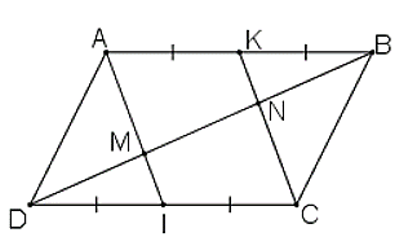
a) ABCD là hình bình hành
⇒ AB // CD ⇒ AB // IC
AB = CD
Mà K, I lần lượt là trung điểm của AB và CD.
⇒AK = IC
Mà AK // IC
⇒ AKIC là hình bình hành
Xét ΔADI và ΔBCKcó:
DI = BK
AI = CK
AD = BC
⇒ ΔADI = ΔBCK (c.c.c)
⇒
Xét ΔADM và ΔCBN có:
AD=BC
( Do AD//BC)
⇒ ΔADM = ΔCBN (g.c.g)Lời giải
Ban đầu Hùng có nhiều hơn Dũng:
5 + 5 = 10 (viên bi).
Số viên bi của bạn Hùng là:
(46 + 10) : 2 = 28 (viên bi).
Số viên bi của bạn Dũng là:
46 – 28 = 18 (viên bi).
Đáp số: Hùng: 28 viên bi; Dũng: 18 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo