Câu hỏi:

19/08/2025 2,002

Cho tam giác ABC (AB < AC) đường cao AH. Gọi M, N, P lần lượt là trung điểm của cạnh BC, CA, AB.

a) Chứng minh NP là đường trung trực của AH.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

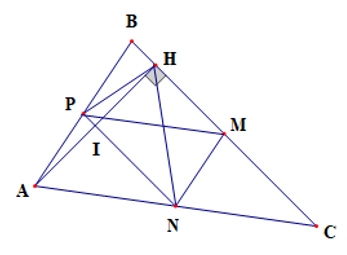
Cho tam giác ABC (AB < AC) đường cao AH. Gọi M, N, P lần lượt là trung điểm của cạnh BC, CA, AB. a) Chứng minh NP là đường trung trực của AH. (ảnh 1)

a) Gọi I là giao điểm của AH và PN

Xét tam giác ABC có P, N là trung điểm của AB, AC

Do đó PN là đường trung bình của tam giác ABC

Suy ra PN // BC

Mà AH ⊥ BC nên PN ⊥ AH (1)

Ta có : PN // BC mà PI thuộc PN nên PI // BC

Xét tam giác AHB có PI // BC và P là trung điểm của AB

Suy ra I là trung điểm của AH (2)

Từ (1) và (2) suy ra PN là đg trung trực của AH.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm x biết $(\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{10}) x = \frac{1}{9} + \frac{2}{8} + \frac{3}{7} + ... + \frac{9}{1} .$

Xem đáp án

Lời giải

Ta có: $\frac{1}{9} + \frac{2}{8} + \frac{3}{7} + ... + \frac{9}{1}$

= \frac{1}{9} + 1 + \frac{2}{8} + 1 + \frac{3}{7} + 1 + ... + \frac{9}{1} + 1 + 1 - 10

= \frac{10}{9} + \frac{10}{8} + \frac{10}{7} + ... + \frac{10}{1} + 1 - 10

= \frac{10}{9} + \frac{10}{8} + \frac{10}{7} + ... + \frac{10}{2} + 1

= 10 (\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{10})

Suy ra

(\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{10}) x = \frac{1}{9} + \frac{2}{8} + \frac{3}{7} + ... + \frac{9}{1}

\Leftrightarrow (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{10}) x = 10 (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{10})

\Leftrightarrow x = 10

Vậy x = 10.

Câu 2

Cho hình thang cân ABCD có đáy lớn AB = 30 cm, đáy nhỏ CD = 10 cm và $\hat{A} = 60 °$ .

a) Tính cạnh BC.

Xem đáp án

Lời giải

. Cho hình thang cân ABCD có đáy lớn AB = 30 cm, đáy nhỏ CD = 10 cm và góc A=60 độ . a) Tính cạnh BC. (ảnh 1)

a) Kẻ CH ⊥ AB, DK ⊥ AB

Suy ra DK // CH (quan hệ từ vuông góc đến song song)

Mà CD // HK

Suy ra CDKH là hình bình hành

Lại có $\hat{C H K} = 90 °$ nên CDKH là hình chữ nhật

Suy ra KH = CD = 10 (cm)

Vì ABCD là hình thang cân nên AD = BC và $\hat{A} = \hat{B} = 60 °$

Xét ∆AKD và ∆BHC có

$\hat{A} = \hat{B}$ (chứng minh trên);

AD = BC (chứng minh trên);

$\hat{A K D} = \hat{B H C} (= 90 °)$

Do đó ∆AKD = ∆BHC (cạnh huyền – góc nhọn)

Suy ra AK = BH

Ta có AB = AK + KH + BH = 30

Hay 2AK + 10 = 30

Suy ra AK = BH = 10 (cm)

Xét tam giác BCH vuông ở H

Suy ra $B C = \frac{B H}{cos \hat{B}} = \frac{10}{cos60 °} = 20$ (cm)

Câu 3