Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: A, B, K thẳng hàng.
Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: A, B, K thẳng hàng.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
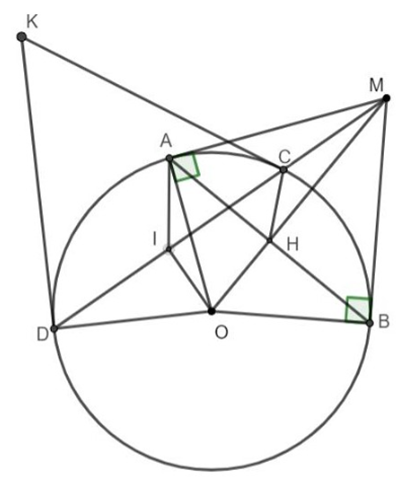
MA là tiếp tuyến của đường tròn (O)
\[\widehat {MAC} = \widehat {MDA}\](góc tạo bởi tiếp tuyến và dây cùng và góc nội tiếp cùng chắn cung AC)
Xét △MAC và △MDA:
\[\widehat {MAC} = \widehat {MDA}\]
\[\widehat M\] chung
Do đó △MAC ᔕ △MDA (g.g)
Suy ra \[\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\]hay MA2 = MC.MD
Xét ∆AMO vuông tại A có AH ^ OM nên ta có:
Þ MH. MO = MA2 (hệ thức lượng trong tam giác)
Þ MH. MO = MC.MD
Mà \[\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\]
Þ △MHC ᔕ △MDC (c.g.c)
\[ \Rightarrow \widehat {MHC} = \widehat {MDO}\]
Þ Tứ giác HCDO nội tiếp đường tròn
Ta có: KC và KD là hai tiếp tuyến cắt nhau tại K của đường tròn (O)
\[ \Rightarrow \widehat {KDO} = \widehat {KCO} = 90^\circ \]
\[ \Rightarrow \widehat {KDO} + \widehat {KCO} = 180^\circ \]
Þ Tứ giác KCOD nội tiếp đường tròn
Mà tứ giác HODC nội tiếp đường tròn
Þ 5 điểm K, C, H, O, D cùng thuộc một đường tròn
Þ HK là phân giác của \[\widehat {CHD}\] (do KC = KD)
Vậy 3 điểm A, B, K thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Các số có hai chữ số có nghĩa là :
1,3.103; 1,3.10−3
Vậy có 2 số có 2 chữ số có nghĩa.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lớp học 100 học sinh được chia làm 3 nhóm:
Không nói được tiếng
Nói được 1 thứ tiếng hoặc Anh hoặc Pháp
Nói được cả 2 thứ tiếng Anh và Pháp
Tổng số học sinh không biết và nói được 1 thứ tiếng là:
100 – 23 = 77 (học sinh)
Số học sinh chỉ nói được tiếng Anh là:
70 – 23 = 47 (học sinh)
Số học sinh nói được tiếng pháp là:
45 – 23 = 22 (học sinh)
Số học sinh nói được tiếng Anh hoặc Pháp là:
47 + 22 = 69 (học sinh)
Ta có số học sinh không biết tiếng và số học sinh chỉ biết 1 thứ tiếng là 77 học sinh. Trong đó 69 học sinh chỉ nói được 1 thứ tiếng.
Số học sinh không biết tiếng Anh hoặc Pháp là:
77 – 69 = 8 (học sinh)
Đáp số: 8 học sinh
Câu 3
\[A.\,\,\overrightarrow a = ( - 5;0),\,\,\overrightarrow b = ( - 4;0)\] cùng hướng.
\[B.\,\,\overrightarrow c = (7;3)\]là vecto đối của \[\overrightarrow d = ( - 7;3)\].
C. \[C.\,\,\overrightarrow u = (4;2)\,,\,\,\overrightarrow v = (8;3)\] cùng phương.
D. \[\overrightarrow a = (6;3)\,,\,\,\overrightarrow b = (2;1)\] ngược hướng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập