Cho biểu thức:
\[A = \left( {\frac{{x - 5\sqrt x }}{{x - 25}} - 1} \right):\left( {\frac{{25 - x}}{{x + 2\sqrt x - 15}} - \frac{{\sqrt x + 3}}{{\sqrt x + 5}} + \frac{{\sqrt x - 5}}{{\sqrt x - 3}}} \right)\]
a) Rút gọn A.
b) Tìm x để A < 1.
Cho biểu thức:
\[A = \left( {\frac{{x - 5\sqrt x }}{{x - 25}} - 1} \right):\left( {\frac{{25 - x}}{{x + 2\sqrt x - 15}} - \frac{{\sqrt x + 3}}{{\sqrt x + 5}} + \frac{{\sqrt x - 5}}{{\sqrt x - 3}}} \right)\]
a) Rút gọn A.
b) Tìm x để A < 1.
Quảng cáo
Trả lời:
Lời giải
ĐKXĐ: x ≥ 0, x ≠ 25, x ≠ 9
a) \[A = \left( {\frac{{x - 5\sqrt x }}{{x - 25}} - 1} \right):\left( {\frac{{25 - x}}{{x + 2\sqrt x - 15}} - \frac{{\sqrt x + 3}}{{\sqrt x + 5}} + \frac{{\sqrt x - 5}}{{\sqrt x - 3}}} \right)\]
\[ = \frac{{x - 5\sqrt x - \left( {x - 25} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}:\left[ {\frac{{25 - x}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}} - \frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}} + \frac{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}} \right]\]
\[ = \frac{{ - 5\left( {\sqrt x - 5} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}:\frac{{25 - x - \left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right) + x - 25}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}\]
\[ = - \frac{5}{{\sqrt x + 5}}:\frac{{ - \left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}\]
\[ = - \frac{5}{{\sqrt x + 5}}.\frac{{ - \left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\]
\[ = - \frac{5}{{\sqrt x + 5}} \cdot \frac{{ - \left( {\sqrt x + 5} \right)}}{{\sqrt x + 3}}\]
\[ = \frac{5}{{\sqrt x + 3}}\].
b) Với x ≥ 0, x ≠ 25, x ≠ 9, ta có
A < 1 \[ \Leftrightarrow \frac{5}{{\sqrt x + 3}} < 1\] ⇔ \[ \Leftrightarrow \frac{{5 - \left( {\sqrt x + 3} \right)}}{{\sqrt x + 3}} < 0 \Leftrightarrow \frac{{2 - \sqrt x }}{{\sqrt x + 3}} < 0\]
\( \Leftrightarrow 2 - \sqrt x < 0\) (vì \[\sqrt x + 3 > 0\] ∀x ≥ 0, x ≠ 25, x ≠ 9)
\( \Leftrightarrow \sqrt x > 2 \Leftrightarrow x > 4\)
Kết hợp điều kiện x ≥ 0, x ≠ 25, x ≠ 9 ta được: x > 4, x ≠ 25, x ≠ 9.
Vậy để A < 1 thì x > 4, x ≠ 25, x ≠ 9
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
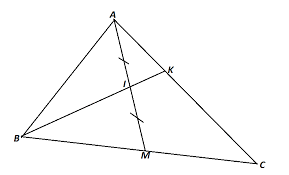
Ta có: \[\left\{ \begin{array}{l}\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} \\\overrightarrow {BI} = \overrightarrow {BM} + \overrightarrow {MI} \end{array} \right.\]
\[ \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} + \left( {\overrightarrow {AI} + \overrightarrow {MI} } \right) = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{{\overrightarrow {BC} }}{2}\]
\[ \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \]
Lại có: \(\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{{\overrightarrow {AC} }}{3}\)
\( \Rightarrow 3\overrightarrow {BK} = 3\overrightarrow {BA} + \overrightarrow {AC} = 2\overrightarrow {BA} + \overrightarrow {BC} \)
Do đó: \(4\overrightarrow {BI} = 3\overrightarrow {BK} \) ⇒ B, I, K thẳng hàng.
Lời giải
Lời giải.
(102 + 112 + 122) : (132 + 142)
= (10 × 10 + 11 × 11 + 12 × 12) : (132 + 142)
= [(12 + 1)2 + (12 + 2)2] : (132 + 142)
= (132 + 142) : (132 + 142)
= 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.