Câu hỏi:
03/07/2023 181
Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh:
a) OM song song O'N;
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO' lớn nhất.
Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh:
a) OM song song O'N;
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO' lớn nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
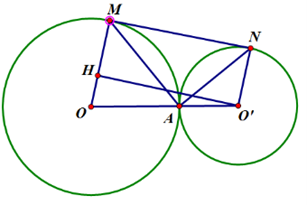
Xét ∆MAN vuông tại A có: \(\widehat {AMN} + \widehat {ANM} = 90^\circ \) (1)
Và \[\widehat {MAO} + \widehat {NAO'} = 90^\circ = 180^\circ - \widehat {MAO} = 180^\circ - 90^\circ = 90^\circ \] (2)
Lại có: ∆OMA cân tại O (OA = OM = R) ⟹ \[\widehat {OAM} = \widehat {OMA}\] (3)
∆O’NA cân tại O (O’A = O’N = R’) ⟹ \[\widehat {O'AN} = \widehat {O'NA}\](4)
Từ (1), (2), (3) và (4) suy ra:
\[\widehat {OMN} + \widehat {MNO'} = \left( {\widehat {OMA} + \widehat {AMN}} \right) + \left( {\widehat {ANM} + \widehat {O'NA}} \right)\]
\[ = \widehat {OMA} + \widehat {AMN} + \widehat {ANM} + \widehat {O'NA}\]
\[ = \widehat {OAM} + \widehat {AMN} + \widehat {ANM} + \widehat {O'AN}\]
\[ = \left( {\widehat {OAM} + \widehat {O'AN}} \right) + \left( {\widehat {AMN} + \widehat {ANM}} \right)\]
\[ = 90^\circ + 90^\circ \]
\[ = 180^\circ \]
Tứ giác OMNO’ có \[\widehat {OMN} + \widehat {MNO'} = 180^\circ \] nên MN // O’N.
b) Từ O’ kẻ O’H ⊥ OM. Khi đó:
\({S_{OMNO'}} = \frac{{\left( {O'N + OM} \right).O'H}}{2} = \frac{{\left( {R' + R} \right).O'H}}{2} \le \frac{{\left( {R' + R} \right).O'O}}{2} = \frac{{{{\left( {R' + R} \right)}^2}}}{2}\)
Dấu bằng xảy ra khi và chỉ khi O’H = O’O hay H ≡ O
⇒ O’O ⊥ MO hoặc O’O ⊥ O’N
Vậy tứ giác MNO’O có diện tích lớn nhất là \(\frac{{{{\left( {R' + R} \right)}^2}}}{2}\) khi O’O ⊥ MO hoặc O’O ⊥ O’N.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
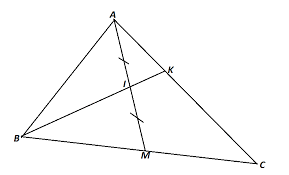
Ta có: \[\left\{ \begin{array}{l}\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} \\\overrightarrow {BI} = \overrightarrow {BM} + \overrightarrow {MI} \end{array} \right.\]
\[ \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} + \left( {\overrightarrow {AI} + \overrightarrow {MI} } \right) = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{{\overrightarrow {BC} }}{2}\]
\[ \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \]
Lại có: \(\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{{\overrightarrow {AC} }}{3}\)
\( \Rightarrow 3\overrightarrow {BK} = 3\overrightarrow {BA} + \overrightarrow {AC} = 2\overrightarrow {BA} + \overrightarrow {BC} \)
Do đó: \(4\overrightarrow {BI} = 3\overrightarrow {BK} \) ⇒ B, I, K thẳng hàng.
Lời giải
Lời giải
Gọi A là biến cố “ba viên bi lấy được chỉ có hai màu”
Ta có: Số phần tử của không gian mẫu: \(C_{16}^3 = 560\)
Số cách chọn được ba viên bi chỉ có một màu: \(C_4^3 + C_5^3 + C_7^3 = 49\)
Số cách chọn được ba viên bi có đủ ba màu: \(C_4^1 + C_5^1 + C_7^1 = 140\)
Vậy xác suất cần tìm là: \({\rm P}\left( A \right) = 1 - \frac{{49 + 140}}{{560}} = \frac{{53}}{{80}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận