Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
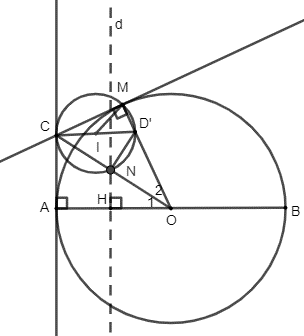
a) Do (I) tiếp xúc với AC tại C nên I ∈ đường thẳng vuông góc với AC tại C
Gọi D’ là giao của đường thẳng vuông góc với AC tại C với OM
Ta có: ∆CMD’ vuông tại M (CM nằm trên đường thẳng tiếp xúc với (O)) (1)
Lại có: (I) qua M và tiếp xúc với AC tại C tức là (I) qua M và C ⇒ IM = IC (2)
Từ (1) và (2) ⇒ I là trung điểm của CD’ (theo định lí về trung điểm và cạnh huyền của tam giác vuông)
⇒ CD’ là đường kính của (I) do ∆CMD’ vuông tại M (3)
Theo giả thiết: CD là đường kính của (I) (4)
Từ (3) và (4) ⇒ D ≡ D’ hay 3 điểm O, M, D thẳng hàng (vì D’ ∈ OM)
b) Do CA và CM là 2 tiếp tuyến của (O) cắt nhau tại C \( \Rightarrow {\widehat O_1} = {\widehat O_2}\) (theo định lí tiếp tuyến thì OC là phân giác của \(\widehat {AOM}\) (5)
Mặt khác: CD ⊥ AC và OA ⊥ AC ⇒ CD // OA \( \Rightarrow {\widehat C_1} = {\widehat O_1}\) (so le trong) (6)
Từ (5) và (6) \( \Rightarrow {\widehat C_1} = {\widehat O_2}\) ⇒ ∆CDO cân tại D
c) Do N ∈ (I) ⇒ \(\widehat {CND} = 90^\circ \) (CN ⊥ ND)
Mặt khác: N ∈ OC ⇒ N là chân đường vuông góc từ D xuống OC
Mà ∆CDO cân tại D nên DN đồng thời là đường trung tuyến ⇒ NC = NO
Gọi (d) là đường thẳng qua N và vuông góc với AB
Gọi H là giao điểm của (d) và AB ⇒ NH ⊥ AB
Xét ∆ACO và ∆HNO có \[\widehat {CAO} = \widehat {NHO} = 90^\circ \], \[{\widehat O_1}\] là góc chung
⇒ ∆ACO đồng dạng với ∆HNO (góc – góc)
⇒ \(\frac{{ON}}{{OC}} = \frac{{OH}}{{OA}} = \frac{1}{2}\) (do NO = NC)
⇒ H là trung điểm của OA (là điểm cố định do OA cố định)
Vậy khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định H.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
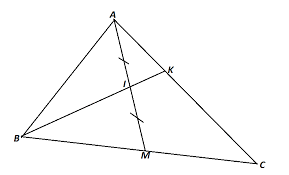
Ta có: \[\left\{ \begin{array}{l}\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} \\\overrightarrow {BI} = \overrightarrow {BM} + \overrightarrow {MI} \end{array} \right.\]
\[ \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} + \left( {\overrightarrow {AI} + \overrightarrow {MI} } \right) = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{{\overrightarrow {BC} }}{2}\]
\[ \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \]
Lại có: \(\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{{\overrightarrow {AC} }}{3}\)
\( \Rightarrow 3\overrightarrow {BK} = 3\overrightarrow {BA} + \overrightarrow {AC} = 2\overrightarrow {BA} + \overrightarrow {BC} \)
Do đó: \(4\overrightarrow {BI} = 3\overrightarrow {BK} \) ⇒ B, I, K thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải.
(102 + 112 + 122) : (132 + 142)
= (10 × 10 + 11 × 11 + 12 × 12) : (132 + 142)
= [(12 + 1)2 + (12 + 2)2] : (132 + 142)
= (132 + 142) : (132 + 142)
= 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập