Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
Quảng cáo
Trả lời:
Lời giải
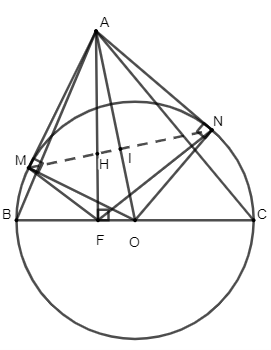
a) \(\widehat {AMO} = \widehat {AFO} = \widehat {ANO} = 90^\circ \)
⇒ A, M, F, N, O cùng thuộc một đường tròn
b) Gọi I là giao của MN và AO nên I là trung điểm của MN ⇒ AI.AO = AM2
Xét ∆AMH và ∆AFM có: \(\widehat {AMH} = \widehat {AFM}\) và \(\widehat {MAH}\) chung nên ∆AMH đồng dạng với ∆AFM
⇒ AH.AF = AM2 = AI.AO
⇒ \(\widehat {AHI} = \widehat {AOF}\) ⇒ OFHI nội tiếp ⇒ M, N, H thẳng hàng
c) Từ câu a) ta có: HM.HN = HA.HF
Ta có: HM.HN = (IM – IH).(IH + IN)
= (IM – IH).(IH + IM)
= IM2 – IH2
= OM2 – OI2 – (OH2 – OI2)
= R2 – OH2
Từ đó suy ra: HA.HF = R2 – OH2.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
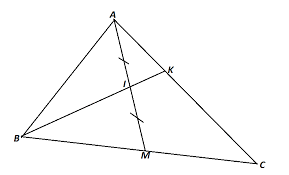
Ta có: \[\left\{ \begin{array}{l}\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} \\\overrightarrow {BI} = \overrightarrow {BM} + \overrightarrow {MI} \end{array} \right.\]
\[ \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} + \left( {\overrightarrow {AI} + \overrightarrow {MI} } \right) = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{{\overrightarrow {BC} }}{2}\]
\[ \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \]
Lại có: \(\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{{\overrightarrow {AC} }}{3}\)
\( \Rightarrow 3\overrightarrow {BK} = 3\overrightarrow {BA} + \overrightarrow {AC} = 2\overrightarrow {BA} + \overrightarrow {BC} \)
Do đó: \(4\overrightarrow {BI} = 3\overrightarrow {BK} \) ⇒ B, I, K thẳng hàng.
Lời giải
Lời giải.
(102 + 112 + 122) : (132 + 142)
= (10 × 10 + 11 × 11 + 12 × 12) : (132 + 142)
= [(12 + 1)2 + (12 + 2)2] : (132 + 142)
= (132 + 142) : (132 + 142)
= 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.