Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Ta có: n4 + 2n3 – n2 – 2n
= (n4 + 2n3) – (n2 + 2n)
= n3(n + 2) – n(n + 2)
= (n3 – n)(n + 2)
= n(n2 – 1)(n + 2)
= (n – 1)n(n + 1)(n + 2)
Ta thấy (n – 1)n(n + 1)(n + 2) là tích bốn số nguyên liên tiếp nên sẽ chứa một số chia hết cho 2 và một số chia hết cho 4, từ đó suy ra tích bốn số nguyên liên tiếp chia hết cho 8.
Đồng thời, trong bốn số nguyên liên tiếp luôn chứa tích của ba số nguyên liên tiếp, đồng nghĩa với việc tích bốn số nguyên liên tiếp chia hết cho 3.
Mà 24 = 3.8
Vì vậy tích bốn số nguyên liên tiếp chia hết cho 3.8 = 24.
Vậy n4 + 2n3 – n2 – 2n chia hết cho 24 với mọi số nguyên n.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
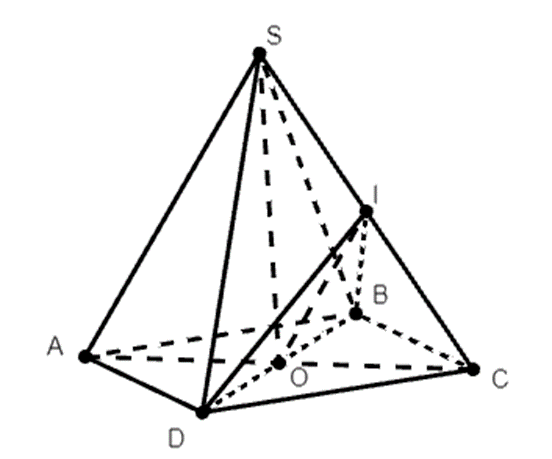
Ta có: IO//SA ⇒ IO//(SAD) và IO//(SAB) nên đáp án A và đáp án C đúng.
Ta có (SAC) ∩ (IBD) = IO nên đáp án D đúng.
Câu B ta có thiết diện là ∆IBD nên B sai.
Lời giải
Chọn 5 học sinh tùy ý trong 11 học sinh có số cách là: \(C_{11}^5\)
\( \Rightarrow n\left( \Omega \right) = 462\)
Gọi A là biến cố chọn ra 5 học sinh trong đó có cả nam và nữ.
Khi đó \(\overline A \) là biến cố chọn ra 5 học sinh trong đó tất cả là nữ hoặc tất cả là nam.
Suy ra n(\(\overline A \)) = \(C_6^5 + C_5^5 = 6 + 1 = 7\) (Cách)
\( \Rightarrow n(A) = n\left( \Omega \right) - n\left( {\overline A } \right) = 462 - 7 = 455\) (cách)
Vậy có 455 cách chọn ra 5 học sinh trong đó có cả nữ và nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.