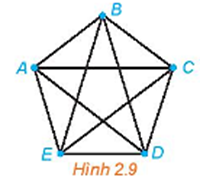
Trước khi vào một hồi nghị, các đại biểu bắt tay nhau (hai người bắt tay nhau nhiều nhất 1 lần). Có một đại biểu không bắt tay ai hết và thấy rằng có 4 người bắt tay 4 lần, 5 người bắt tay 5 lần và 6 người bắt tay 6 lần. Nếu hội nghị có đúng 16 đại biểu thì ông ta đếm nhầm. Vì sao có thể kết luận như vậy?
Quảng cáo
Trả lời:
Lời giải:
Những kiến thức ban đầu về lí thuyết đồ thị trong bài học này sẽ giúp chúng ta tìm được câu trả lời cho tình huống trên như sau:
Ta vẽ một đồ thị với 16 đỉnh tương ứng với 16 đại biểu tham dự hội nghị. Nếu hai đại biểu nào bắt tay nhau thì ta nối hai đỉnh tương ứng bằng một cạnh.
Theo số liệu mà đại biểu đếm số bắt tay cung cấp, ta có một đồ thị với 16 đỉnh, trong đó có 1 đỉnh bậc 0, 4 đỉnh bậc 4, 5 đỉnh bậc 5 và 6 đỉnh bậc 6.
Ở đây số đỉnh bậc 5 là 5, là một số lẻ. Điều này mâu thuẫn với hệ quả của Định lí bắt tay (Số đỉnh bậc lẻ của mọi đồ thị là một số chẵn).
Vậy đại biểu đó đã đếm sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.
Khi đó, ta có số đỉnh bậc 4 là: 12 – x.
Tổng số bậc của các đỉnh là: 3x + 4(12 – x).
Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là 28 . 2 = 56.
Do đó, ta có phương trình 3x + 4(12 – x) = 56, tức là 8 + x = 0. Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.
Lời giải
Lời giải:
Hình biểu diễn của đồ thị G như sau.
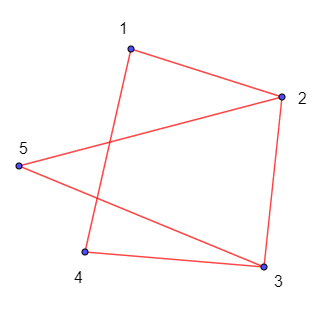
Đồ thị G là đơn đồ thị, nhưng không phải đồ thị đầy đủ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.