Quảng cáo
Trả lời:
Lời giải:
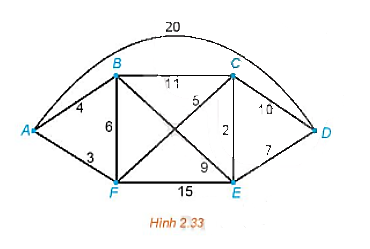
Đầu tiên, ta gắn nhãn đỉnh A là I(A) = 0 và gắn cho ba đỉnh kề với A là B, F và D các nhãn tạm thời I(A) + 4, I(A) + 3 và I(A) + 20. Chọn số nhỏ nhất trong chúng và viết I(F) = 3. Đỉnh F bây giờ được gắn nhãn vĩnh viễn là 3.
Tiếp theo, ta gắn cho các đỉnh kề với F là B, C và E các nhãn tạm thời I(F) + 6, I(F) + 5 và I(F) + 15 (B hiện có hai nhãn tạm thời là 4 và 9). Nhãn tạm thời nhỏ nhất trong các nhãn đã gán (ở B, C, E) hiện nay là 4 (tại B), nên ta viết I(B) = 4. Đỉnh B được gắn nhãn vĩnh viễn là 4.
Bây giờ ta xét các đỉnh kề với B (mà chưa được gắn nhãn vĩnh viễn) là C và E. Ta gắn cho đỉnh C nhãn tạm thời là I(B) + 11 (hiện C có hai nhãn tạm thời là 8 và 15), gắn cho đỉnh E nhãn tạm thời là I(B) + 9 (E hiện có hai nhãn tạm thời là 18 và 13. Nhãn tạm thời nhỏ nhất bây giờ là 8 (tại C), do đó ta viết I(C) = 8.
Bây giờ ta xét các đỉnh kề với C (mà chưa được gắn nhãn vĩnh viễn) là E và D. Ta gắn nhãn cho đỉnh E tạm thời là I(C) + 2 (hiện E có ba nhãn tạm thời là 18, 13 và 10), gắn cho đỉnh D nhãn tạm thời là I(C) + 10. Nhãn tạm thời nhỏ nhất bây giờ là 10 (tại E), do đó ta viết I(E) = 10.
Xét đỉnh kề với E là D, ta gắn cho D nhãn tạm thời I(E) + 7 (hiện D có hai nhãn tạm thời là 18 và 17). Vậy đỉnh D sẽ được gắn nhãn vĩnh viễn là 17 hay I(D) = 17.
Vì I(D) = 17 nên đường đi ngắn nhất từ A đến D có độ dài là 17.
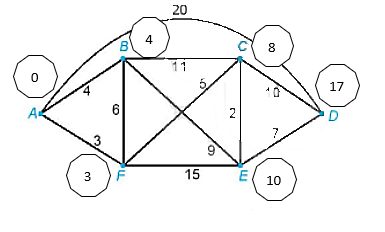
Để tìm một đường đi ngắn nhất từ A đến D như vậy, ta sẽ lần ngược từ điểm cuối D. Ta chỉ cần giới hạn ở việc xét những cạnh mà độ dài là hiệu của các nhãn gắn tại đầu các mút của nó, đó là DE, EC, CF và FA (do I(D) – I(E) = 17 = 10 = 7, I(E) – I(C) = 10 – 8 = 2, I(C) – I(F) = 8 – 3 = 5 và I(F) – I(A) = 3 – 0 = 3).
Khi đó ta có thể kết luận, đường đi ngắn nhất từ A đến D phải đi qua các cạnh DE, EC, CF và FA.
Vậy, đường đi ngắn nhất (trong trường hợp này là duy nhất) từ A đến D là
A → F → C → E → D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
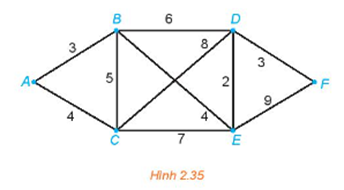
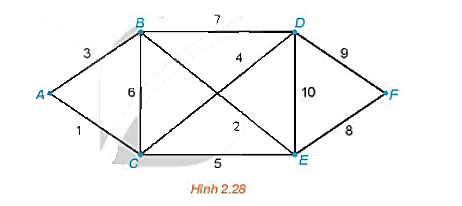
Vì đồ thị Hình 2.35 là liên thông và các đỉnh đều có bậc chẵn (ở đây chỉ có đỉnh A và đỉnh F có bậc là 2, các đỉnh còn lại đều có bậc 4) nên đồ thị này có chu trình Euler.
Một chu trình Euler xuất phát từ đỉnh A là ABCDBEDFECA và tổng độ dài của nó là
3 + 5 + 8 + 6 + 4 + 2 + 3 + 9 + 7 + 4 = 51.
Vậy một chu trình cần tìm là ABCDBEDFECA và có độ dài là 51.
Lời giải
Lời giải:
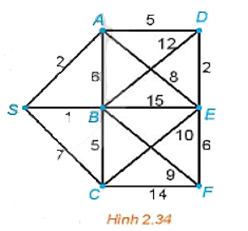
Đồ thị Hình 2.32 chỉ có hai đỉnh bậc lẻ là A và D nên ta có thể tìm được một đường đi Euler từ A đến D (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ A đến D là AFEABEDBCD và tổng độ dài của nó là
10 + 9 + 7 + 2 + 8 + 16 + 15 + 3 + 4 = 74.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ D đến A theo thuật toán gắn nhãn vĩnh viễn.
Đường đi ngắn nhất từ D đến A là DCBA và có độ dài là 4 + 3 + 2 = 9.
Vậy một chu trình cần tìm là AFEABEDBCDCBA và có độ dài là 74 + 9 = 83.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.