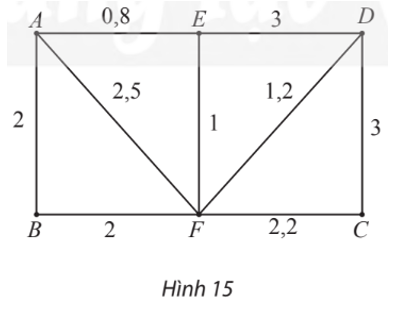
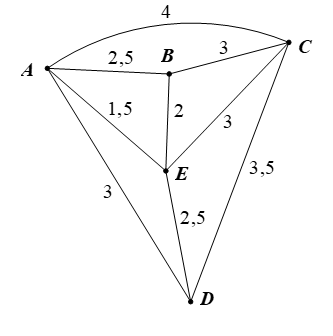
Bảng 2 cho biết thời gian di chuyển tính bằng giờ của các tuyến xe buýt giữa các bến xe A, B, C, D, E (số nằm tại ô giao của hàng và cột là số giờ cần để xe buýt đi từ bến này đến bến kia, dấu û biểu thị giữa hai bến này không có tuyến xe buýt). Hãy vẽ một đồ thị có trọng số biểu diễn các tuyến xe buýt cùng thời gian di chuyển của mỗi tuyến.
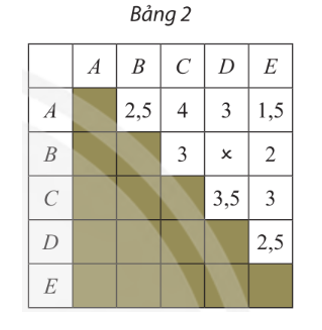
Bảng 2 cho biết thời gian di chuyển tính bằng giờ của các tuyến xe buýt giữa các bến xe A, B, C, D, E (số nằm tại ô giao của hàng và cột là số giờ cần để xe buýt đi từ bến này đến bến kia, dấu û biểu thị giữa hai bến này không có tuyến xe buýt). Hãy vẽ một đồ thị có trọng số biểu diễn các tuyến xe buýt cùng thời gian di chuyển của mỗi tuyến.

Quảng cáo
Trả lời:
Đồ thị có trọng số như hình vẽ sau thỏa mãn yêu cầu bài toán, trong đó các đỉnh biểu diễn các bến xe, các cạnh biểu diễn các tuyến xe buýt giữa các bến xe (nếu có), trọng số của mỗi cạnh biểu diễn thời gian di chuyển tính bằng giờ của tuyến xe buýt tương ứng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
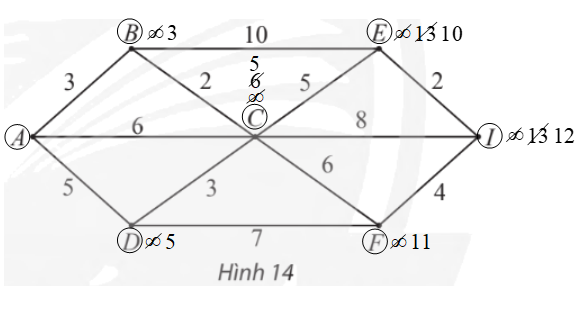
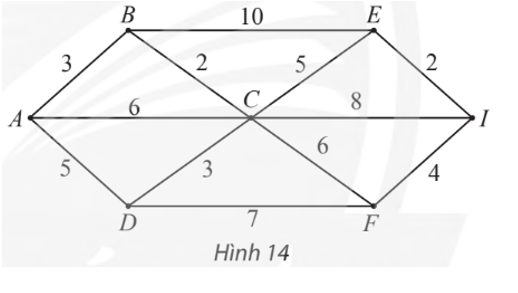
– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm B, C, D, ta có:
⦁ nB = nA + wAB = 0 + 3 = 3. Vì 3 < ∞ nên ta đổi nhãn của B thành 3.
⦁ nC = nA + wAC = 0 + 6 = 6. Vì 6 < ∞ nên ta đổi nhãn của C thành 6.
⦁ nD = nA + wAD = 0 + 5 = 5. Vì 5 < ∞ nên ta đổi nhãn của D thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần đỉnh A nhất, chỉ tính các đỉnh khác đỉnh A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm C, E, ta có:
⦁ nC = nB + wBC = 3 + 2 = 5. Vì 5 < 6 (6 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 5.
⦁ nE = nB + wBE = 3 + 10 = 13. Vì 13 < ∞ nên ta đổi nhãn của E thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C, D (đều có nhãn là 5) nên ta tùy ý khoanh tròn đỉnh C (đỉnh gần đỉnh A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh C gồm E, D, F, I, ta có:
⦁ nE = nC + wCE = 5 + 5 = 10. Vì 10 < 13 (13 là nhãn hiện tại của E) nên ta đổi nhãn của E thành 10.
⦁ nD = nC + wCD = 5 + 3 = 8. Vì 8 > 5 (5 là nhãn hiện tại của D) nên ta giữ nguyên nhãn của D là 5.
⦁ nF = nC + wCF = 5 + 6 = 11. Vì 11 < ∞ nên ta đổi nhãn của F thành 11.
⦁ nI = nC + wCI = 5 + 8 = 13. Vì 13 < ∞ nên ta đổi nhãn của I thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta khoanh tròn đỉnh D (đỉnh gần đỉnh A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ có đỉnh F, ta có:
nF = nD + wDF = 5 + 7 = 12.
Vì 12 > 11 (11 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 11.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần đỉnh A thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E chỉ có đỉnh I, ta có:
nI = nE + wEI = 10 + 2 = 12.
Vì 12 < 13 (13 là nhãn hiện tại của I) nên ta đổi nhãn của I thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ năm).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F chỉ còn đỉnh I, ta có:
nI = nF + wFI = 11 + 4 = 15.
Vì 15 > 12 (12 là nhãn hiện tại của I) nên ta giữ nguyên nhãn của I là 12.
Lúc này, ta thấy chỉ còn đỉnh I chưa được khoanh tròn nên ta khoanh tròn đỉnh I (đỉnh gần A thứ sáu).
– Nhìn ngược lại các bước trên, ta thấy:
nI = 12 = nE + wEI
= nC + wCE + wEI
= nB + wBC + wCE + wEI
= nA + wAB + wBC + wCE + wEI
= wAB + wBC + wCE + wEI
= lABCEI.
Vậy ABCEI là đường đi ngắn nhất từ A đến I, với độ dài bằng 12.
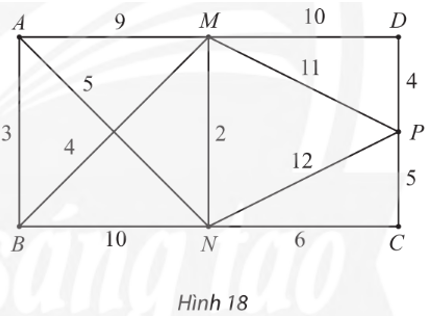
Lời giải
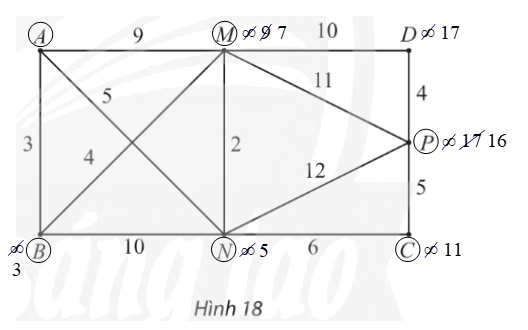
– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với đỉnh A, gồm M, N, B, ta có:
⦁ nM = nA + wAM = 0 + 9 = 9. Vì 9 < ∞ nên ta đổi nhãn của M thành 9.
⦁ nN = nA + wAN = 0 + 5 = 5. Vì 5 < ∞ nên ta đổi nhãn của N thành 5.
⦁ nB = nA + wAB = 0 + 3 = 3. Vì 3 < ∞ nên ta đổi nhãn của B thành 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A nhất, chỉ tính các đỉnh khác A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm M, N, ta có:
⦁ nM = nB + wBM = 3 + 4 = 7. Vì 7 < 9 (9 là nhãn hiện tại của M) nên ta đổi nhãn của M thành 7.
⦁ nN = nB + wBN = 3 + 10 = 13. Vì 13 > 5 (5 là nhãn hiện tại của N) nên ta giữ nguyên nhãn của N là 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là N nên ta khoanh tròn đỉnh N (đỉnh gần A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh N gồm M, C, P, ta có:
⦁ nM = nN + wNM = 5 + 2 = 7. Vì 7 cũng là nhãn hiện tại của M nên ta giữ nguyên nhãn của M là 7.
⦁ nC = nN + wNC = 5 + 6 = 11. Vì 11 < ∞ nên ta đổi nhãn của C thành 11.
⦁ nP = nN + wNP = 5 + 12 = 17. Vì 17 < ∞ nên ta đổi nhãn của P thành 17.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là M nên ta khoanh tròn đỉnh M (đỉnh gần A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh M gồm D, P, ta có:
⦁ nD = nM + wMD = 7 + 10 = 17. Vì 17 < ∞ nên ta đổi nhãn của D thành 17.
⦁ nP = nM + wMP = 7 + 11 = 18. Vì 18 > 17 (17 là nhãn hiện tại của P) nên ta giữ nguyên nhãn của P là 17.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh C chỉ có đỉnh P, ta có:
nP = nC + wCP = 11 + 5 = 16. Vì 16 < 17 (17 là nhãn hiện tại của P) nên ta đổi nhãn của P thành 16.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh P nên ta khoanh tròn đỉnh P (đỉnh gần A thứ năm).
– Nhìn lại các bước trên, ta thấy:
nP = 16 = nC + wCP
= nN + wNC + wCP
= nA + wAN + wNC + wCP
= wAN + wNC + wCP
= lANCP.
Vậy ANCP là đường đi ngắn nhất từ đỉnh A đến P, với độ dài bằng 16.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.