Câu hỏi:
13/07/2024 1,060
Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh DABD = DACD.
b) Chứng minh rằng AM = 2.BD.
c) Tính số đo \[\widehat {MAD}\].
Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh DABD = DACD.
b) Chứng minh rằng AM = 2.BD.
c) Tính số đo \[\widehat {MAD}\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
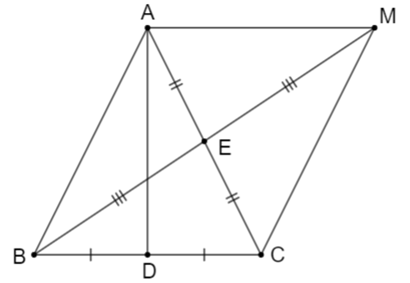
a) Xét tam giác ABD và tam giác ACD có:
AB = AC (gt)
AD: cạnh chung
BD = CD (Do D là chung điểm của BC)
Do đó DABD = DACD (c.c.c)
b) Tứ giác ABCD có E là giao điểm của hai đường chéo AC và BM
Mà AE = EC; BE = EM nên suy ra ABCD là hình bình hành.
Þ AM = BC = 2.BD (đpcm)
c) Tam giác ABC có AB = AC nên ABC là tam giác cân tại A có D là trung điểm của BC nên AD là đường cao
Þ AD ^ BC
Mà AMCB là hình bình hành nên ta có AM // BC
Suy ra AD ^ AM.
Vậy \(\widehat {MAD} = 90^\circ \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1; 17]. Tính xác suất để ba số được viết ra có tổng chia hết cho 3.
Xem đáp án »
12/07/2024
15,112
Câu 2:
Từ các chữ số 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên có năm chữ số khác nhau và nhất thiết phải có chữ số 1 và 5?
Xem đáp án »
13/07/2024
11,112
Câu 3:
Trong mặt phẳng Oxy cho A(−2m; − m), B(2m; m). Với giá trị nào của m thì đường thẳng AB đi qua O?
Xem đáp án »
12/07/2024
8,595
Câu 4:
Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được:
Xem đáp án »
12/07/2024
8,150
Câu 5:
Cho một cấp số cộng (un) có u1 = 5 và tổng 50 số hạng đầu bằng 5150. Tìm công thức của số hạng tổng quát un.
Xem đáp án »
13/07/2024
7,657
Câu 6:
Tìm m để phương trình log2 x + log x − m = 0 có 2 nghiệm phân biệt thuộc khoảng (0; 1).
Xem đáp án »
13/07/2024
5,862
Câu 7:
Chứng minh: \(\sqrt {{a^2} + {b^2}} + \sqrt {{c^2} + {d^2}} \ge \sqrt {{{\left( {a + c} \right)}^2} + {{\left( {b + d} \right)}^2}} ,\;\forall a,\;b,\;c,\;d \in \mathbb{R}\).
Xem đáp án »
13/07/2024
4,458
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận