Cho mặt phẳng (Q) và điểm M nằm ngoài mặt phẳng (Q).

a) Trong mặt phẳng (Q) vẽ hai đường thẳng a’, b’ cắt nhau. Qua điểm M kẻ các đường thẳng a và b lần lượt song song với a’, b’. Gọi (P) là mặt phẳng xác định bởi hai đường thẳng (cắt nhau) a và b (Hình 63). Mặt phẳng (P) có song song với mặt phẳng (Q) hay không?

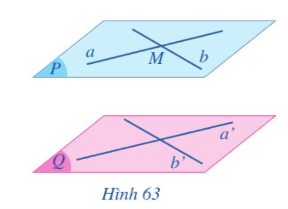
b) Xét mặt phẳng (R) đi qua điểm M và song song với mặt phẳng (Q). Hai mặt phẳng (R) và (P) có trùng nhau hay không?

Lời giải

a)

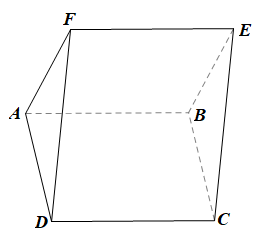
Ta có: BE // AF (do ABEF là hình bình hành);

            AF ⊂ (AFD)

Do đó BE // (AFD).

Ta cũng có: BC // AD (do ABCD là hình bình hành)

                    AD ⊂ (AFD)

Do đó BC // (AFD).

Do BE // (AFD);

      BC // (AFD);

      BE, BC cắt nhau tại điểm B và cùng nằm trong mp(BEC)

Suy ra (AFD) // (BEC).

b)

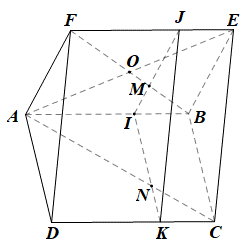
+) Do (AFD) song song với (P) nên tồn tại hai đường thẳng trong (AFD) song song với (P).

• Trong mp(ABEF), qua điểm M vẽ đường thẳng song song với AF, đường thẳng này cắt AB, EF lần lượt tại I, J.

Khi đó IJ // AF, mà AF ⊂ (AFD) nên IJ // (AFD).

• Trong mp(ABCD), qua điểm I vẽ đường thẳng song song với AD, cắt CD tại K.

Khi đó IK // AD, mà AD ⊂ (AFD) nên IK // (AFD).

• Ta có: IJ // (AFD);

             IK // (AFD);

             IJ, IK cắt nhau tại điểm I và cùng nằm trong mp(IJK).

Do đó (IJK) // (AFD).

Mà M ∈ IJ, IJ ⊂ (IJK) nên mp (P) đi qua M và song song với (AFD) chính là mp(IJK).

+) Trong mp(ABCD), AC cắt IK tại N, khi đó N là giao điểm của AC và (P).

Trong mp(ABCD), xét DABC có IN // BC (do IK // AD // BC) nên theo định lí Thalès ta có: \[\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}}\].

Trong mp(ABEF), xét DABF có IM // AF nên theo định lí Thalès ta có: \[\frac{{AI}}{{IB}} = \frac{{FM}}{{MB}}\].

Gọi O là tâm hình bình hành ABEF. Khi đó O là trung điểm của FB nên FO = OB.

Do M là trọng tâm của DABE nên \(MB = \frac{2}{3}OB\) và \(OM = \frac{1}{3}OB\).

Ta có: \[\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}} = \frac{{FM}}{{MB}} = \frac{{FO + OM}}{{MB}} = \frac{{OB + \frac{1}{3}OB}}{{\frac{2}{3}OB}} = \frac{{\frac{4}{3}OB}}{{\frac{2}{3}OB}} = 2\].

Vậy \(\frac{{AM}}{{NC}} = 2\).

Lời giải

a)

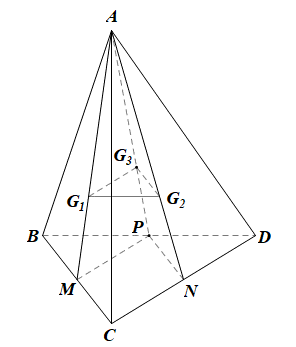
Gọi M, N, P lần lượt là trung điểm của BC, CD, DB.

Trong mp(ABC), xét DABC có G₁ là trọng tâm của tam giác nên \(\frac{{A{G_1}}}{{AM}} = \frac{2}{3}\);

Trong mp(ACD), xét DACD có G₂ là trọng tâm của tam giác nên \(\frac{{A{G_2}}}{{AN}} = \frac{2}{3}\);

Trong mp(ABD), xét DABD có G₃ là trọng tâm của tam giác nên \(\frac{{A{G_3}}}{{AP}} = \frac{2}{3}\).

Trong mp(AMP), xét DAMP có \(\frac{{A{G_1}}}{{AM}} = \frac{{A{G_3}}}{{AP}} = \frac{2}{3}\) nên G₁G₃­ // MP (theo định lí Thalès đảo).

Mà MP ⊂ (BCD) nên G₁G₃­ // (BCD).

Chứng minh tương tự ta cũng có \[\frac{{A{G_2}}}{{AN}} = \frac{{A{G_3}}}{{AP}} = \frac{2}{3}\] nên G₂G₃ // NP (theo định lí Thalès đảo).

Mà NP ⊂ (BCD) nên G₂G₃­ // (BCD).

Ta có: G₁G₃­ // (BCD);

           G₂G₃­ // (BCD);

           G₁G₃, G₂G₃ cắt nhau tại G₃ và cùng nằm trong mp(G₁G₂G₃).

Do đó (G₁G₂G₃) // (BCD).

b)

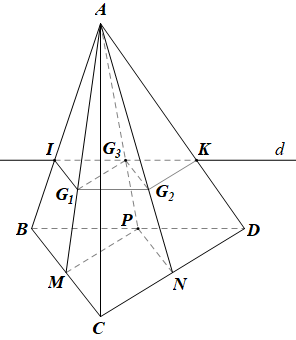
Ta có: B, D cùng thuộc hai mặt phẳng (ABD) và (BCD) nên (ABD) ∩ (BCD) = BD.

Giả sử (ABD) ∩ (G₁G₂G₃) = d.

Ta có: (G₁G₂G₃) // (BCD);

           (ABD) ∩ (BCD) = BD;

           (ABD) ∩ (G₁G₂G₃) = d.

Suy ra d // BD.

Mà G₃ ∈ (ABD) và G₃ ∈ (G₁G₂G₃) nên G_3­ là giao điểm của (G₁G₂G₃) và (ABD).

Do đó giao tuyến d của hai mặt phẳng (G₁G₂G₃) và (ABD) đi qua điểm G₃ và song song với BD, cắt AB, AD lần lượt tại I và K.

Vậy (G₁G₂G₃) ∩ (ABD) = IK.