Câu hỏi:
13/07/2024 2,510
b) Chị An cho rằng có khoảng 25% số lần sạc điện thoại chỉ dùng được dưới 10 giờ. Nhận định của chị An có hợp lí không?
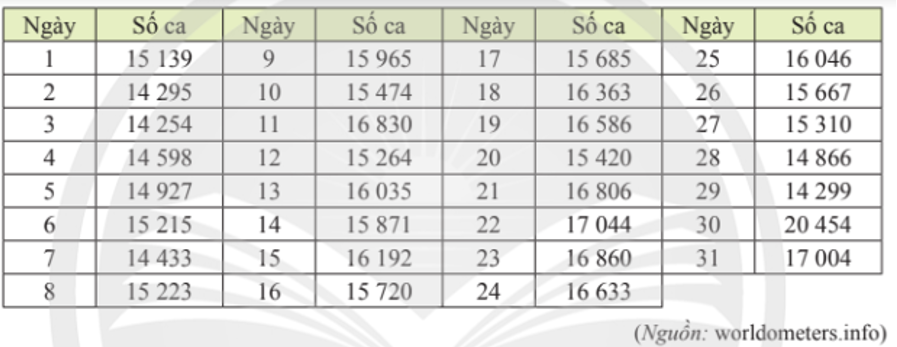
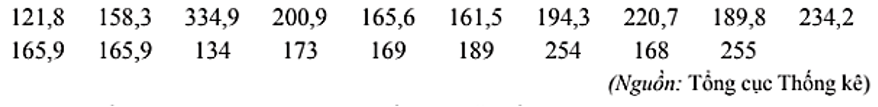b) Chị An cho rằng có khoảng 25% số lần sạc điện thoại chỉ dùng được dưới 10 giờ. Nhận định của chị An có hợp lí không?
Câu hỏi trong đề: Giải SGK Toán 11 CTST Bài tập cuối chương V có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
b) Tổng số lần sử dụng là: 2 + 5 + 7 + 6 + 3 = 23 (lần).
Gọi x1; ...; x23 là thời gian sử dụng của pin điện thoại mới sau mỗi lần theo thứ tự không giảm.
Ta có: x1; x2 ∈ [7; 9), x3; ...; x7 ∈ [9; 11), x8; ...; x14 ∈ [11; 13), x15; ...; x20 ∈ [13; 15), x21; x22; x23 ∈ [15; 17).
Tứ phân vị thứ nhất là x6 ∈ [9; 11) nên ta có: .
Do đó nhận định có 25% số lần sạc điện thoại chỉ dùng dưới 10 giờ là nhận định hợp lí.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có bảng giá trị đại diện:
|
Khoảng điểm |
[6,5; 7) |
[7; 7,5) |
[7,5; 8) |
[8; 8,5) |
[8,5; 9) |
[9; 9,5) |
[9,5; 10) |
|
Giá trị đại diện |
6,75 |
7,25 |
7,75 |
8,25 |
8,75 |
9,25 |
9,75 |
|
Tần số |
8 |
10 |
16 |
24 |
13 |
7 |
4 |
+) Ước lượng trung bình của mẫu số liệu là:
.
+) Gọi x1; ...; x82 là điểm trung bình môn Toán của một số học sinh lớp 11 được sắp xếp theo chiều ko giảm.
Ta có: x1; ...; x8 ∈ [6,5; 7), x9; ...; x18 ∈ [7; 7,5), x19; ...; x34 ∈ [7,5; 8), x35; ...; x58 ∈ [8; 8,5), x59; ...; x71 ∈ [8,5; 9), x72; ...; x78 ∈ [9; 9,5), x79; ...; x82 ∈ [9,5; 10).
Trung vị của mẫu số liệu là và x41; x42 ∈ [8; 8,5) nên ta có:
.
+) Mốt của mẫu số liệu thuộc khoảng [8; 8,5) nên:
.
Lời giải
Đáp án đúng là: B
Ta có bảng giá trị đại diện sau:
|
Doanh thu |
[5; 7) |
[7; 9) |
[9; 11) |
[11; 13) |
[13; 15) |
|
Giá trị đại diện |
6 |
8 |
10 |
12 |
14 |
|
Số ngày |
2 |
7 |
7 |
3 |
1 |
Giá trị trung bình của mẫu số liệu là:
∈ [9; 11).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo