Câu hỏi:

12/07/2024 5,877

Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có sơ đồ Ven, ta có:

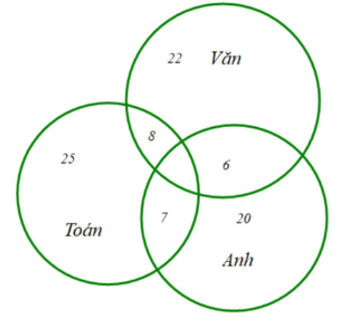
Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh? (ảnh 1)

Số học sinh giỏi ít nhất hai môn là:

7 + 6 + 8 = 21 (em)

Số học sinh giỏi cả ba môn Toán, Văn, Anh là:

22 + 25 + 20 – 40 – 21 = 6 (em)

Đáp số: 6 em.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD.

Xem đáp án

Lời giải

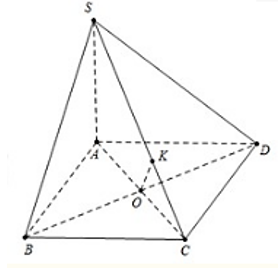
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD. (ảnh 1)

Gọi O là tâm hình vuông ABCD

Ta có: AC ^ BD; BD ^ SA

Do đó BD ^ (SAC)

Dựng OK ^ SC

Do đó OK là đoạn vuông góc chung của BD và SC

Khi đó $d (B D; S C) = O K = \frac{1}{2} d (A; S C)$ $= \frac{1}{2} \cdot \frac{S A . A C}{\sqrt{S A^{2} + A C^{2}}}$ (1)

Ta có: AC2 = AB2 + BC2 = 2a2

Suy ra $A C = a \sqrt{2}$

Thay vào (1) ta có $d = \frac{a \sqrt{6}}{6}$ .

Vậy $d = \frac{a \sqrt{6}}{6}$ .

Câu 2

Tìm tập hợp tất cả các giá trị của tham số m để hàm số:

y = x³ − mx²− (m − 6)x + 1 đồng biến trên (0; 4).

Xem đáp án

Lời giải

Ta có y^’ = 3x² – 2mx – (m – 6)

Để hàm số đồng biến trên (0; 4)

Û y’ ≥ 0 "x Î (0; 4) và y′ = 0 tại một số giá trị hữu hạn.

3x² − 2mx − (m − 6) ≥ 0 ∀x ∈ (0; 4)

⇔ 3x²+ 6 ≥ m(2x + 1)

Với mọi x ∈ (0; 4) ta có 2x + 1 > 0 nên

$f (x) = \frac{3 x^{2} + 6}{2 x + 1} \geq m \forall x \in (0; 4)$

⇔ m ≤ min_{(0; 4)} của f(x)

Xét hàm số $f (x) = \frac{3 x^{2} + 6}{2 x + 1}$ trên (0; 4) ta có:

$f^{'} (x) = \frac{6 x^{2} + 6 x - 12}{{(2 x + 1)}^{2}} = 0$

$\Leftrightarrow [\begin{matrix} x = 1 \in (0; 4) \\ x = - 2 \notin (0; 4) \end{matrix}$

Xét bảng biến thiên:

Tìm tập hợp tất cả các giá trị của tham số m để hàm số: y = x^3 − mx^2 − (m − 6)x + 1 đồng biến trên (0; 4). (ảnh 1)

Dựa vào bảng biến thiên ta thấy min_{(0; 4)} của f(x) = f(1) = 3 Û m ≤ 3

Khi m = 3 ta có : y′ = 3x² − 6x + 3 = 3(x − 1)² ≥ 0 ∀x ∈ (0;4)

Vậy với m ≤ 3 thì hàm số đồng biến trên (0; 4).

Câu 3