Câu hỏi:
03/08/2023 875
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a2. Hình chiếu của đỉnh A’ trên mặt đáy (ABCD) là điểm H thỏa mãn . Biết rằng . Tính góc giữa mặt phẳng (ADA’) và mặt phẳng (ABCD)
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a2. Hình chiếu của đỉnh A’ trên mặt đáy (ABCD) là điểm H thỏa mãn . Biết rằng . Tính góc giữa mặt phẳng (ADA’) và mặt phẳng (ABCD)
Đáp án chính xác
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
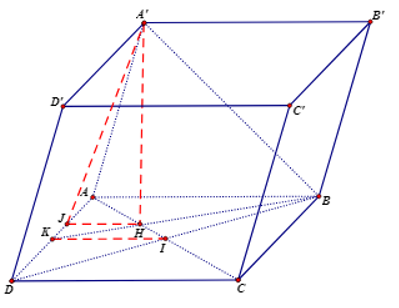
Xét tam giác ABD có và AI là trung tuyến nên H là trọng tâm tam giác
Kéo dài BH cắt AD tại K
Suy ra K là trung điểm của AD và
Vì SABCD = 9a2 nên AB = BC = CD = DA = 3a
Xét tam giác ABK vuông ở A có BK2 = AB2 + AK2
Suy ra
Trong mp(ABCD) dựng HJ // AB (J ∈ AD)
Suy ra AD ⊥ HJ (1)
Mà AD ⊥ HA’, do đó AD ⊥ (A’HJ)
Suy ra AD ⊥ A’J (2)
Ta có (A’AD) ∩ (ABCD) = AD (3)
Từ (1), (2) và (3) suy ra
Xét tam giác A’HB vuông tại H có A’B2 = HB2 + A’H2
Suy ra
Xét tam giác AKI có KI // JH
Suy ra
Do đó
Xét tam giác A’HB vuông tại H có JH = A’H = a
Suy ra tam giác A’HJ vuông cân tại H
Do đó
Vậy ta chọn đáp án A.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật và C là tập hợp các hình vuông. Khi đó:
Cho A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật và C là tập hợp các hình vuông. Khi đó:
Xem đáp án »
03/08/2023
17,731
Câu 5:
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?
Xem đáp án »
03/08/2023
4,361
Câu 6:
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D, O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh tứ giác MAOB nội tiếp.
b) Chứng minh MB2 = MC . MD.
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là tia phân giác của .
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D, O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh tứ giác MAOB nội tiếp.
b) Chứng minh MB2 = MC . MD.
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là tia phân giác của .
Xem đáp án »
11/07/2024
4,091
Câu 7:
Tính tổng tất cả các nghiệm thực của phương trình:
A. ;
B. 6;
C. ;
D. 9.
Xem đáp án »
12/07/2024
3,521
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận