Câu hỏi:
13/07/2024 155
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng A B C D trùng với trọng tâm G của tam giác ABD. Đường thẳng SD tạo với mặt phẳng một góc 60°. Tính khoảng cách giữa hai đường thẳng AB và SC.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng A B C D trùng với trọng tâm G của tam giác ABD. Đường thẳng SD tạo với mặt phẳng một góc 60°. Tính khoảng cách giữa hai đường thẳng AB và SC.
Câu hỏi trong đề:
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
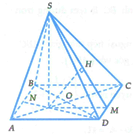
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN.
Tam giác SGD vuông tại G nên nhọn.
Do SG ^ (ABCD) nên
Tam giác NAD vuông tại A nên .
Suy ra
Do đó
Ta có CD // AB mà CD Ì (SCD) nên AB // (SCD).
Ta có:
Suy ra
Từ G kẻ đường thẳng song song với AD, cắt CD tại M thì CD ^ (SGM)
Suy ra (SCD) ^ (SGM).
Hai mặt phẳng (SCD) và (SGM) cắt nhau theo giao tuyến SM.
Từ G kẻ GH ^ SM, H Î SM thì GH ^ (SCD).
Do đó d(G; (SCD)) = GH
Ta có: và tam giác SGM vuông tại G có đường cao GH nên
.
Vậy .
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai số phức z1, z2 thỏa mãn các điều kiện |z1| = |z2| = 2 và |z1 + 2z2| = 4. Tính giá trị của |2z1 − z2|.
Cho hai số phức z1, z2 thỏa mãn các điều kiện |z1| = |z2| = 2 và |z1 + 2z2| = 4. Tính giá trị của |2z1 − z2|.
Xem đáp án »
13/07/2024
14,521
Câu 4:
Cho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Tìm thiết diện của mặt phẳng (P) và tứ diện ABCD.
Cho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Tìm thiết diện của mặt phẳng (P) và tứ diện ABCD.
Xem đáp án »
23/08/2023
5,697
Câu 5:
Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính theo a diện tích xung quanh của hình trụ.
Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính theo a diện tích xung quanh của hình trụ.
Xem đáp án »
13/07/2024
5,043
Câu 6:
Tìm tất cả các giá trị của tham số m để hàm số y = −x3 + 2x2 − mx + 1 đạt cực tiểu tại x = 1.
Tìm tất cả các giá trị của tham số m để hàm số y = −x3 + 2x2 − mx + 1 đạt cực tiểu tại x = 1.
Xem đáp án »
13/07/2024
4,797
về câu hỏi!