Câu hỏi:

29/11/2023 759

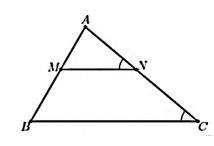
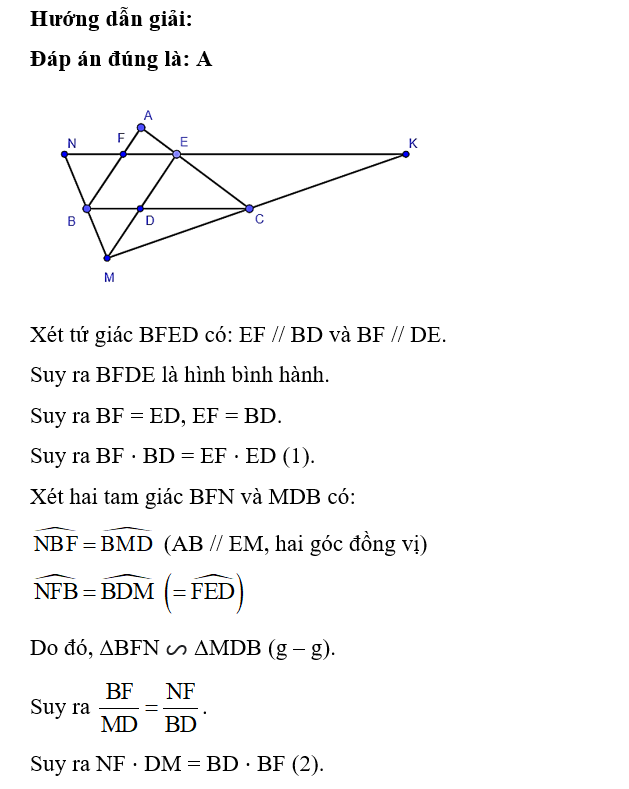
Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường thẳng song song với AB và BC, lần lượt cắt d tại M và N. Gọi D là giao điểm của ME và BC. Đường thẳng NE cắt AB và MC lần lượt tại F và K. Khi đó tam giác AFN đồng dạng với tam giác nào dưới đây?

A. Tam giác MDC;

B. Tam giác DNC;

C. Tam giác ACM;

D. Tam giác NKB.

Xem lời giải

Câu hỏi trong đề: 10 Bài tập Trường hợp đồng dạng thứ ba của tam giác (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường (ảnh 1)

Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường (ảnh 2)

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình bình hành ABCD có AC > BD. Kẻ CE ⊥ AB tại E, CF ⊥ AD tại F, BH ⊥ AC tại H và DK ⊥ AC tại K. Khẳng định nào sau đây là đúng?

A. AD ⋅ AB + AE ⋅ AF = AC²;

B. AB ⋅ AF + AE ⋅ AD = AC²;

C. AD ⋅ AF + AE ⋅ AB = AC²;

D. AD ⋅ AF ⋅ AE ⋅ AB = AC².

Lời giải

Hướng dẫn giải:

Đáp án đúng là: C

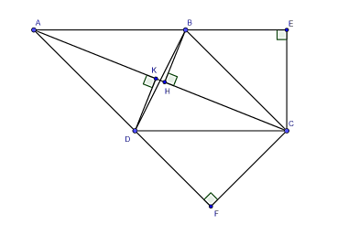
Cho hình bình hành ABCD có AC > BD. Kẻ CE vuông góc AB tại E, CF vuông góc AD tại F (ảnh 1)

Xét tam giác AKD vuông tại K và tam giác CHB vuông tại H có:

AD = BC (do ABCD là hình bình hành)

$\hat{D A K} = \hat{B C H}$ (AD // BC, hai góc so le trong)

Do đó, ∆AKD = ∆CHB (cạnh huyền – góc nhọn).

Suy ra AK = HC.

Xét hai tam giác AHB và AEC có:

$\hat{AHB} = \hat{AEC} = 90 °$

$\hat{EAC}$ : Góc chung

Do đó, ΔAHB ᔕ ΔAEC (g – g).

Suy ra $\frac{AB}{AC} = \frac{AH}{AE}$ .

Suy ra AB ⋅ AE = AC ⋅ AH (1).

Xét hai tam giác ADK và ACF có

$\hat{AKD} = \hat{AFC} = 90 °$

$\hat{FAC}$ : Góc chung

Do đó, ΔADK ᔕ ΔACF (g – g).

Suy ra $\frac{AD}{AC} = \frac{AK}{AF}$ .

Suy ra AD ⋅ AF = AC ⋅ AK (2).

Lấy (1) + (2) ta được AB ⋅ AE + AD ⋅ AF = AC ⋅ AH + AC ⋅ AK

Lại có AC ⋅ AH + AC ⋅ AK = AC ⋅ (AH + AK) = AC ⋅ (AH + HC) = AC ⋅ AC = AC².

Vậy AB ⋅ AE + AD ⋅ AF = AC².

Câu 2

Cho hình bình hành ABCD. Một đường thẳng bất kì đi qua A cắt BD tại E và cắt các đường thẳng BC, CD lần lượt tại F và G. Trong các khẳng định sau, khẳng định nào là sai?

A. ΔABF ᔕ ΔEGD;

B. ΔGCF ᔕ ΔGDA;

C. ΔGCF ᔕ ΔABF

D. ΔABF ᔕ ΔGDA;

Lời giải

Hướng dẫn giải:

Đáp án đúng là: A

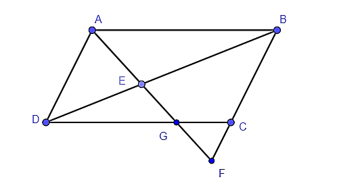
Cho hình bình hành ABCD. Một đường thẳng bất kì đi qua A cắt BD tại E và cắt các đường thẳng BC (ảnh 1)

Xét hai tam giác GCF và GDA có:

$\hat{AGD} = \hat{FGC}$ (đối đỉnh)

$\hat{DAG} = \hat{GFC}$ (AD // BF, hai góc so le trong)

Suy ra ΔGCF ᔕ ΔGDA (g – g) (1).

Xét hai tam giác GCF và ABF có:

$\hat{F}$ : Góc chung

$\hat{FCG} = \hat{FBA}$ (GC // BA, hai góc đồng vị)

Suy ra ΔGCF ᔕ ΔABF (g – g) (2).

Từ (1) và (2) suy ra ΔGDA ᔕ ΔABF.

Vậy A sai.

Câu 3

Cho tam giác ABC có đường phân giác trong AD. Gọi M và N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. Khi đó tỉ số $\frac{AB}{AC}$ bằng tỉ số

A. $\frac{AD}{CN}$ ;

B. $\frac{ND}{CN}$ ;

C. $\frac{BM}{CN}$ ;

\frac{BD}{CN}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình vẽ sau. Khẳng định nào dưới đây là sai?

A. ΔAMN ᔕ ΔABC;

B. AM ⋅ AN = AC ⋅ AB;

C. MN // BC;

D. AM ⋅ AC = AN ⋅ AB.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABC vuông tại A, đường cao AH. Khi đó BH ⋅ BC bằng

A. AB;

B. HC²;

C. AC²;

D. AB².

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình vẽ, độ dài cạnh DC bằng

A. 7 cm;

B. 8 cm;

C. 9 cm;

D. 10 cm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho hình bình hành ABCD có AC > BD. Kẻ CE ⊥ AB tại E, CF ⊥ AD tại F, BH ⊥ AC tại H và DK ⊥ AC tại K. Khẳng định nào sau đây là đúng?

Cho hình bình hành ABCD. Một đường thẳng bất kì đi qua A cắt BD tại E và cắt các đường thẳng BC, CD lần lượt tại F và G. Trong các khẳng định sau, khẳng định nào là sai?

Cho tam giác ABC có đường phân giác trong AD. Gọi M và N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. Khi đó tỉ số ABAC bằng tỉ số

Cho hình vẽ sau. Khẳng định nào dưới đây là sai?

Cho tam giác ABC vuông tại A, đường cao AH. Khi đó BH ⋅ BC bằng

Cho hình vẽ, độ dài cạnh DC bằng

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác ABC có đường phân giác trong AD. Gọi M và N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. Khi đó tỉ số $\frac{AB}{AC}$ bằng tỉ số