Câu hỏi:
13/07/2024 1,353
Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (một sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó loại xe A có 10 chiếc, loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng.
Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (một sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó loại xe A có 10 chiếc, loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng.
Câu hỏi trong đề:
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x là số xe loại A được thuê, y là số xe loại B được thuê. (x ≥ 0, y ≥ 0)
Do loại xe A có 10 chiếc, loại xe B có 9 chiếc nên x ≤ 10, y ≤ 9.
Do xe A chỉ chở tối đa 20 người và 0,6 tấn hàng, xe B chở tối đa 10 người và 1,5 tấn hàng mà cần thuê xe để chở trên 140 người và trên 9 tấn hàng nên:
Khi đó ta có hệ bất phương trình của x và y như sau:
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy:
- Biểu diễn miền nghiệm D1 của bất phương trình x ≥ 0.
+ Đường thẳng x = 0 là trục Oy.
Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy (kể cả bờ Oy) nằm bên phải trục Oy.
* Tương tự ta biểu diễn các miền nghiệm:
- Miền nghiệm D2 của bất phương trình y ≥ 0: là nửa mặt phẳng bờ Ox (kể cả bờ Ox) nẳm bên trên trục Ox.
- Miền nghiệm D3 của bất phương trình x ≤ 10: là nửa mặt phẳng bờ d1 (kể cả bờ d1: x = 10) chứa điểm O.
- Miền nghiệm D4 của bất phương trình y ≤ 9: là nửa mặt phẳng bờ d2 (kể cả bờ d2: y = 9) chứa điểm O.
- Miền nghiệm D5 của bất phương trình 2x + y ≥ 14:
+ Vẽ đường thẳng d3: 2x + y = 14.
+ Xét điểm O(0; 0): thay x = 0, y = 0 vào bất phương trình ta có 2. 0 + 0 = 0 ≥ 14 là mệnh đề sai nên điểm O(0; 0) không thỏa mãn bất phương trình 2x + y ≥ 14.
Miền nghiệm D5 của bất phương trình 2x + y ≥ 14 là nửa mặt phẳng bờ d3 (kể cả bờ d3) không chứa điểm O.
- Tương tự miền nghiệm D6 của bất phương trình 2x + 5y ≥ 30 là nửa mặt phẳng bờ d4 (kể cả bờ d4: 2x + 5y = 30) không chứa điểm O.
Ta có đồ thị:
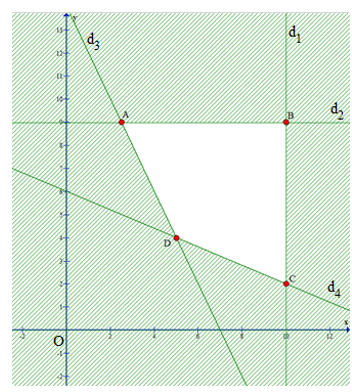
Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD:
A(2,5; 9), B(10; 9), C(10; 2), D(5; 4)
Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu nên tổng số tiền thuê là:
F (x; y) = 4x + 3y.
Để chi phí vận chuyển là thấp nhất thì F (x; y) là nhỏ nhất.
Tại A(2,5; 9): F = 4. 2,5 + 3. 9 = 37;
Tại B(10; 9): F = 4. 10 + 3. 9 = 67;
Tại C(10; 2): F = 4. 10 + 3. 2 = 46;
Tại D(5; 4): F = 4. 5 + 3. 4 = 32;
Vậy F (x; y) đạt giá trị nhỏ nhất là 32 khi x = 5 và y = 4.
Vậy cần thuê 5 xe loại A và 4 xe loại B để số tiền thuê nhỏ nhất.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
1 chiếc đồng hồ đánh chuông, kể từ thời điểm 0 giờ thì sau mỗi giờ số tiếng chuông đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. hỏi một ngày đồng hồ đánh bao nhiêu tiếng chuông?
1 chiếc đồng hồ đánh chuông, kể từ thời điểm 0 giờ thì sau mỗi giờ số tiếng chuông đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. hỏi một ngày đồng hồ đánh bao nhiêu tiếng chuông?
Xem đáp án »
13/07/2024
15,816
Câu 3:
Gọi m là giá trị lớn nhất của hàm sô y = 3 + 2sin2x trên đoạn . Giá trị m là bao nhiêu?
Gọi m là giá trị lớn nhất của hàm sô y = 3 + 2sin2x trên đoạn . Giá trị m là bao nhiêu?
Xem đáp án »
13/07/2024
5,397
Câu 4:
Để đo chiều cao của một tòa nhà, bác Nam lấy hai điểm A và D trên mặt đất có khoảng cách AD = 10m cùng thẳng hàng với chân B của tòa nhà để đặt hai giác kế. Chân của giác kế có chiều cao 1,2m. Gọi C là đỉnh của tòa nhà và hai điểm A1 và D1, là đỉnh của hai giác kế cùng thẳng hàng với điểm B1 thuộc chiều cao BC của tòa nhà. Bác đo được các góc = 35°, = 40°. Hỏi chiều cao của tòa nhà là bao nhiêu?
Để đo chiều cao của một tòa nhà, bác Nam lấy hai điểm A và D trên mặt đất có khoảng cách AD = 10m cùng thẳng hàng với chân B của tòa nhà để đặt hai giác kế. Chân của giác kế có chiều cao 1,2m. Gọi C là đỉnh của tòa nhà và hai điểm A1 và D1, là đỉnh của hai giác kế cùng thẳng hàng với điểm B1 thuộc chiều cao BC của tòa nhà. Bác đo được các góc = 35°, = 40°. Hỏi chiều cao của tòa nhà là bao nhiêu?
Xem đáp án »
13/07/2024
4,546
Câu 5:
Gọi S là tập các giá trị m ≠ 0 để parabol (P): y = mx2 + 2mx + m2 + 2m có đỉnh nằm trên đường thẳng y = x + 7. Tính tổng các giá trị tập S.
Gọi S là tập các giá trị m ≠ 0 để parabol (P): y = mx2 + 2mx + m2 + 2m có đỉnh nằm trên đường thẳng y = x + 7. Tính tổng các giá trị tập S.
Xem đáp án »
13/07/2024
4,455
Câu 7:
Lớp 10A có 40 học sinh trong đó có 10 bạn học sinh giỏi Toán, 15 bạn học sinh giỏi Lý và 19 bạn không giỏi môn học nào trong hai môn Toán, Lý. Hỏi lớp 10A có bao nhiêu bạn học sinh vừa giỏi Toán vừa giỏi Lý?
Xem đáp án »
13/07/2024
3,508
Bình luận
🔥 Đề thi HOT:
-
53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
120 câu Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1)
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
về câu hỏi!