Câu hỏi:
12/07/2024 1,799
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ $t$ của năm $2017$ được cho bởi một hàm số $y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10$ với $t \in \mathbb{Z}$ và $0 < t \leqslant 365$. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ $t$ của năm $2017$ được cho bởi một hàm số $y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10$ với $t \in \mathbb{Z}$ và $0 < t \leqslant 365$. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Câu hỏi trong đề: Đề kiểm tra Giữa kì 1 Toán 11 CTST có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì $\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] \leqslant 1 \Rightarrow y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10 \leqslant 14.$
Ngày có ánh sáng mặt trời nhiều nhất khi và chỉ khi
$y = 14 \Leftrightarrow \sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] = 1$
$ \Leftrightarrow \frac{\pi }{{178}}\left( {t - 60} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 149 + 356k.$
Do $0 < t \leqslant 365 \Rightarrow 0 < 149 + 356k \leqslant 365$
$ \Leftrightarrow - \frac{{149}}{{356}} < k \leqslant \frac{{54}}{{89}}$.
Mà $k \in \mathbb{Z}$ nên $k = 0$.
Với $k = 0 \Rightarrow t = 149$ rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện $0 < t \leqslant 365$ thì ta biết năm này tháng 2 chỉ có 28 ngày).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
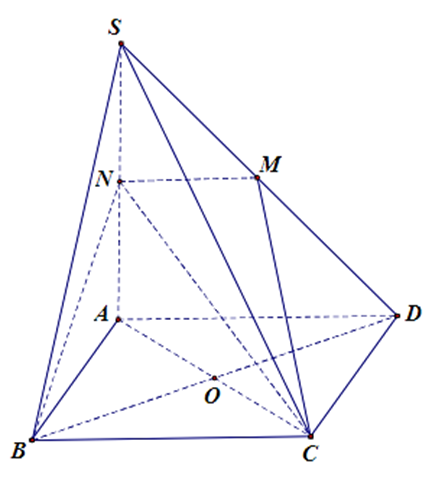
Khi đó $\left\{ \begin{gathered}
O \in AC \hfill \\
O \in ND \subset (SBD) \hfill \\
\end{gathered} \right.$.
Vậy $O$ là giao điểm của $AC$ và mặt phẳng $(SBD)$.
b) Ta có:
• \[(NBC) \cap (ABCD) = BC\]
• $(NBC) \cap (SBC) = BC$
• $(NBC) \cap (SAB) = NB$
• $\left\{ \begin{gathered}
N \in (NBC) \hfill \\
N \in (SAD) \hfill \\
\end{gathered} \right.$ (1)
• $(NBC) \supset BC\,{\text{//}}\,(SAD)$ (2)
Từ (1) và (2) suy ra \[(NBC) \cap \,\,(SAD) = NM\,{\text{//}}\,AD\,{\text{//}}\,BC\].
• \[(NBC) \cap \,\,(SCD) = MC\].
Vậy thiết diện là hình thang $MNCD.$
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận