Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H. Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái TTH. Tính xác suất của biến cố sau:
F: “Trong ba chữ cái, có nhiều nhất hai chữ T”.
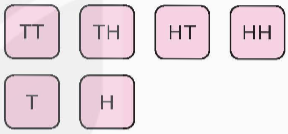
Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H. Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái TTH. Tính xác suất của biến cố sau:
F: “Trong ba chữ cái, có nhiều nhất hai chữ T”.

Quảng cáo
Trả lời:
Phép thử là rút ngẫu nhiên từ mỗi túi một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước.
Kết quả của phép thử là abc với ab là hai chữ cái từ túi I và c là chữ cái từ túi II.
Ta liệt kê tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Túi II Túi I |
T |
H |
|
TT |
TTT |
TTH |
|
TH |
THT |
THH |
|
HT |
HTT |
HTH |
|
HH |
HHT |
HHH |
Mỗi ô trong bảng trên là một kết quả có thể. Các kết quả có thể này là đồng khả năng. Không gian mẫu là Ω = {TTT; TTH; THT; THH; HTT; HTH; HHT; HHH}.
Không gian mẫu có 8 phần tử.
Có 7 kết quả thuận lợi cho biến cố E là: TTH; THT; THH; HTT; HTH; HHT; HHH.
Vậy 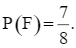
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phép thử là gieo đồng thời hai con xúc xắc cân đối và đồng chất I và II.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là số chấm xuất hiện trên con xúc xắc I và con xúc xắc II.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Xúc xắc II Xúc xắc I |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 36 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); …; (5, 6); (6, 6)}.
Tập Ω có 36 phần tử.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
⦁ Có 25 kết quả thuận lợi của biến cố G là: (1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5). Do đó, 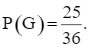
⦁ Có 6 kết quả thuận lợi của biến cố H là: (1, 5); (1, 6); (3, 5); (3, 6); (5, 5); (5, 6). Do đó 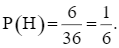
⦁ Có 16 kết quả thuận lợi của biến cố K là: (3, 3); (3, 4); (3, 5); (3, 6); (4, 3); (4, 4); (4, 5); (4, 6); (5, 3); (5, 4); (5, 5); (5, 6); (6, 3); (6, 4); (6, 5); (6, 6). Do đó, 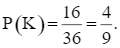
Lời giải
Vì hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa nên các kết quả có thể của phép thử là đồng khả năng.
⦁ Có 3 kết quả thuận lợi của biến cố E là: (A, A); (B, B); (C, C). Do đó, 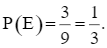
⦁ Có 4 kết quả thuận lợi của biến cố F là: (A, A); (A, B); (B, A); (B, B). Do đó, 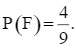
⦁ Có 5 kết quả thuận lợi của biến cố G là: (A, B); (B, A); (B, B); (B, C); (C, B). Do đó, 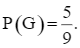
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.