Câu hỏi:
13/07/2024 89
Quan sát cây tìm kiếm nhị phân trong hình 9.1, cùng trao đổi, thảo luận các câu hỏi sau:
a) Nếu thực hiện thuật toán duyệt giữa (trái – gốc – phải) thì nút đầu tiên được duyệt là nút nào?
b) Nút cuối cùng được duyệt là nút nào?
c) Thứ tự các nút được duyệt theo thuật toán duyệt giữa sẽ theo thứ tự nào? Em có nhận xét gì về kết quả đạt được? Giải thích vì sao.
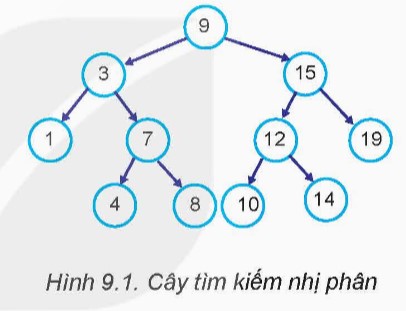
Quan sát cây tìm kiếm nhị phân trong hình 9.1, cùng trao đổi, thảo luận các câu hỏi sau:
a) Nếu thực hiện thuật toán duyệt giữa (trái – gốc – phải) thì nút đầu tiên được duyệt là nút nào?
b) Nút cuối cùng được duyệt là nút nào?
c) Thứ tự các nút được duyệt theo thuật toán duyệt giữa sẽ theo thứ tự nào? Em có nhận xét gì về kết quả đạt được? Giải thích vì sao.
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Nút đầu tiên: Khi thực hiện thuật toán duyệt giữa, nút đầu tiên được duyệt là nút ‘1’, vì nó là nút nằm xa nhất về bên trái của cây.
b) Nút cuối cùng: Nút cuối cùng được duyệt là nút ‘19’, vì nó là nút nằm xa nhất về bên phải của cây.
c) Thứ tự duyệt: Các nút sẽ được duyệt theo thứ tự sau: 1, 3, 4, 7, 8, 9, 10, 12, 15, 14, 19. Kết quả này cho thấy thuật toán duyệt giữa trên cây tìm kiếm nhị phân sẽ cho ra danh sách các nút theo thứ tự tăng dần. Điều này xảy ra bởi vì thuật toán này luôn tuân theo quy tắc: trước tiên duyệt tất cả các nút nhỏ hơn nút gốc (bên trái), sau đó là nút gốc (ở giữa), và cuối cùng là tất cả các nút lớn hơn nút gốc (bên phải).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Thuật toán sắp xếp dãy sử dụng cây tìm kiếm nhị phân có độ phức tạp thời gian là bao nhiêu?
Thuật toán sắp xếp dãy sử dụng cây tìm kiếm nhị phân có độ phức tạp thời gian là bao nhiêu?
Xem đáp án »
13/07/2024
418
Câu 3:
Cho trước dãy số A = [2,1,9,0,2,1,5]. Tạo cây tìm kiếm nhị phân T từ dãy A và thực hiện thuật toán duyệt giữa trên cây T. Em hãy cho biết kết quả duyệt là dãy các khoá có thứ tự như thế nào.
Cho trước dãy số A = [2,1,9,0,2,1,5]. Tạo cây tìm kiếm nhị phân T từ dãy A và thực hiện thuật toán duyệt giữa trên cây T. Em hãy cho biết kết quả duyệt là dãy các khoá có thứ tự như thế nào.
Xem đáp án »
13/07/2024
190
Câu 4:
Trao đổi, thảo luận để giải bài toán sau:
Cho trước dãy số A. Thiết kế thuật toán sắp xếp lại dãy A theo thứ tự tăng dần hoặc giảm dần.
Trao đổi, thảo luận để giải bài toán sau:
Cho trước dãy số A. Thiết kế thuật toán sắp xếp lại dãy A theo thứ tự tăng dần hoặc giảm dần.
Xem đáp án »
13/07/2024
117
Câu 5:
Dựa trên hàm BSTSort(A) đã biết, viết chương trình sắp xếp dãy số giảm dần theo kĩ thuật sử dụng cây tìm kiếm nhị phân.
Dựa trên hàm BSTSort(A) đã biết, viết chương trình sắp xếp dãy số giảm dần theo kĩ thuật sử dụng cây tìm kiếm nhị phân.
Xem đáp án »
13/07/2024
83
Câu 6:
Quan sát cách cài đặt các thuật toán duyệt trên cây tìm kiếm nhị phân và trao đổi về ý nghĩa và sự khác biệt khi thực hiện các thuật toán này so với các thuật toán duyệt cây nhị phân đã học trong Bài 6.
Quan sát cách cài đặt các thuật toán duyệt trên cây tìm kiếm nhị phân và trao đổi về ý nghĩa và sự khác biệt khi thực hiện các thuật toán này so với các thuật toán duyệt cây nhị phân đã học trong Bài 6.
Xem đáp án »
13/07/2024
70
Bình luận
🔥 Đề thi HOT:
-
Đề thi học kì 1 Tin học 12 Kết nối tri thức có đáp án- Đề 1
-
263 câu Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Tin học Chủ đề F. Giải quyết vấn đề với sự trợ giúp của máy tính có đáp án
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 7 có đáp án
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 10 có đáp án
-
Đề thi học kì 1 Tin học 12 Kết nối tri thức có đáp án- Đề 2
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 8 có đáp án
-
Đề thi học kì 1 Tin học 12 Kết nối tri thức có đáp án- Đề 3
-
15 câu Trắc nghiệm Tin học 12 Kết nối tri thức Bài 9 có đáp án
về câu hỏi!