Quan sát cây tìm kiếm nhị phân trong hình 9.1, cùng trao đổi, thảo luận các câu hỏi sau:

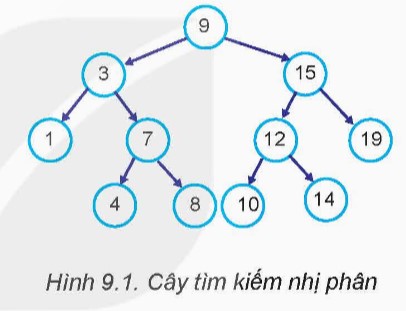
a) Nếu thực hiện thuật toán duyệt giữa (trái – gốc – phải) thì nút đầu tiên được duyệt là nút nào?

b) Nút cuối cùng được duyệt là nút nào?

c) Thứ tự các nút được duyệt theo thuật toán duyệt giữa sẽ theo thứ tự nào? Em có nhận xét gì về kết quả đạt được? Giải thích vì sao.

Quan sát cách cài đặt các thuật toán duyệt trên cây tìm kiếm nhị phân và trao đổi về ý nghĩa và sự khác biệt khi thực hiện các thuật toán này so với các thuật toán duyệt cây nhị phân đã học trong Bài 6.

Cho trước dãy số A = [2,1,9,0,2,1,5]. Tạo cây tìm kiếm nhị phân T từ dãy A và thực hiện thuật toán duyệt giữa trên cây T. Em hãy cho biết kết quả duyệt là dãy các khoá có thứ tự như thế nào.

Với cây T như Câu 1, nếu thực hiện thuật toán duyệt ngược thì thứ tự các khoá thể hiện trên màn hình như thế nào?

Trao đổi, thảo luận để giải bài toán sau:

Cho trước dãy số A. Thiết kế thuật toán sắp xếp lại dãy A theo thứ tự tăng dần hoặc giảm dần.

Viết lại hàm BSTSort(A) thực hiện sắp xếp dãy số A theo thứ tự tăng dần nhưng kết quả không cập nhật vào A. Hàm trả lại dãy số mới là dãy vừa được sắp xếp (gồm các phần tử của dãy A).

Nếu không cần cập nhật vào dãy A mà chỉ cần in ra màn hình các phần tử của A theo thứ tự tăng dần thì cần sửa lại chương trình sắp xếp trên như thế nào?

Dựa trên hàm BSTSort(A) đã biết, viết chương trình sắp xếp dãy số giảm dần theo kĩ thuật sử dụng cây tìm kiếm nhị phân.

Thuật toán sắp xếp dãy sử dụng cây tìm kiếm nhị phân có độ phức tạp thời gian là bao nhiêu?

Dựa trên tính chất của cây tìm kiếm nhị phân, hãy viết hàm minimum(T) và maximum(T) tính giá trị khoá nhỏ nhất và lớn nhất của cây tìm kiếm nhị phân T. 

Viết hàm height(T) tính chiều cao của cây tìm kiếm nhị phân T.