Giải chuyên đề Tin 12 KNTT Bài 16: Kĩ thuật duyệt đồ thị theo chiều rộng có đáp án

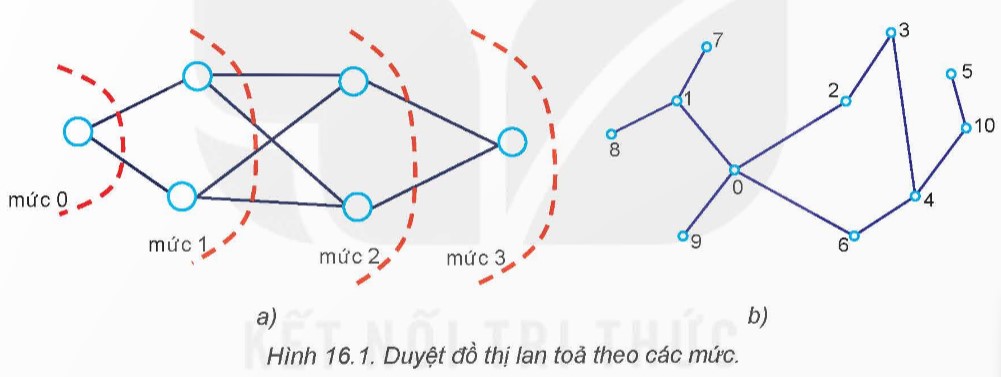
Thuật toán duyệt theo chiều rộng (BFS) bắt đầu từ một đỉnh và duyệt qua tất cả các đỉnh kề với nó trước, sau đó mới chuyển sang các đỉnh kề của các đỉnh đã duyệt. Khi duyệt từ đỉnh 0 của đồ thị Hình 16.1b, chúng ta sẽ tuân theo nguyên tắc sau:

- Nguyên tắc duyệt:

• Duyệt tất cả các đỉnh kề với đỉnh hiện tại trước khi chuyển sang đỉnh kề tiếp theo.
• Sử dụng hàng đợi (queue) để lưu trữ thứ tự duyệt.

- Thứ tự duyệt có thể là:

• Bắt đầu từ đỉnh 0, thăm tất cả các đỉnh kề với đỉnh 0.
• Sau đó, duyệt qua các đỉnh kề với các đỉnh đã thăm theo thứ tự từ hàng đợi.
• Tiếp tục quá trình này cho đến khi tất cả các đỉnh đều được thăm.

Để thực hiện duyệt theo chiều rộng (BFS) từ đỉnh 0 của đồ thị, chúng ta sẽ tuân theo các bước sau:

- Mức 0: Bắt đầu từ đỉnh 0.

- Mức 1: Duyệt tất cả các đỉnh kề với đỉnh 0.

- Mức 2: Duyệt tất cả các đỉnh kề với các đỉnh ở Mức 1 và không phải là đỉnh 0.

- Các Mức tiếp theo: Tiếp tục duyệt các đỉnh kề với đỉnh ở mức trước đó, không lặp lại các đỉnh đã duyệt.

Quá trình này tiếp tục cho đến khi tất cả các đỉnh có thể tiếp cận từ đỉnh 0 đều được duyệt.

Sự khác biệt chính giữa hai phương pháp duyệt đồ thị theo chiều sâu (DFS) và chiều rộng (BFS) là:

- DFS: Duyệt sâu vào từng nhánh của đồ thị trước khi quay lại (backtrack).

- BFS: Duyệt đồ thị theo từng mức độ rộng, từ gần đến xa so với điểm bắt đầu.

Mệnh đề sau là đúng.

- Lý do:

Mệnh đề này có thể được chứng minh tương tự như cách chứng minh tính chất của DFS đối với đường đi trong đồ thị. Cụ thể:

- Chứng minh:

Chúng ta cần chứng minh hai điều sau:

1. Nếu tồn tại đường đi từ đỉnh sss đến đỉnh v, thì quá trình duyệt BFS từ đỉnh sss sẽ duyệt qua đỉnh v.

2. Nếu quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v, thì tồn tại đường đi từ đỉnh sss đến đỉnh v.

- Chứng minh điều 1:

Nếu tồn tại đường đi từ đỉnh s đến đỉnh v:

- Giả sử tồn tại một đường đi từ đỉnh sss đến đỉnhv. Điều này có nghĩa là có một dãy các đỉnh s=v0,v1,v2,…,vk sao cho (vi,vi+1) ∈ E

- Khi thực hiện BFS từ đỉnh sss, BFS sẽ thăm tất cả các đỉnh mà nó có thể truy cập được từ sss. BFS duyệt các đỉnh theo từng mức (level) một cách rộng nhất có thể trước khi chuyển sang mức tiếp theo.

- Điều này bao gồm các đỉnh v1,v2,…,vk vì chúng liên tiếp nhau trong đường đi từ s đến v.

- Do đó, nếu tồn tại đường đi từ đỉnh s đến đỉnh v, BFS sẽ chắc chắn thăm đỉnh v trong quá trình duyệt.

- Chứng minh điều 2:

Nếu quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v:

- Giả sử quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v. Điều này có nghĩa là BFS đã bắt đầu từ đỉnh sss và theo các cạnh của đồ thị, nó đã đến đỉnh v.

- BFS duyệt đồ thị bằng cách đi theo các cạnh của đồ thị, nên mỗi bước từ đỉnh hiện tại đến đỉnh tiếp theo trong quá trình duyệt BFS đều là di chuyển qua các cạnh của đồ thị.

- Nếu BFS đã thăm đỉnh v từ đỉnh s, điều đó có nghĩa là có một dãy các đỉnh bắt đầu từ sss và kết thúc tại v sao cho mỗi đỉnh trong dãy này đều có cạnh nối với đỉnh tiếp theo trong dãy.

- Do đó, tồn tại một đường đi từ đỉnh s đến đỉnh v.

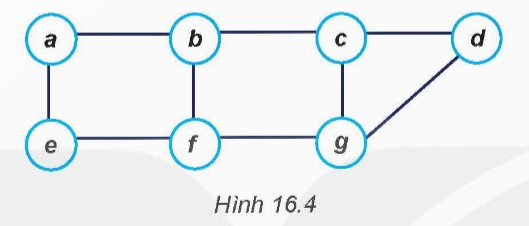
a) Các đỉnh kề với a:

Đỉnh ‘b’, ‘c’ là các đỉnh kề với đỉnh ‘a’.

b) Khoảng cách từ a đến e:

Khoảng cách ngắn nhất từ đỉnh ‘a’ đến đỉnh ‘e’ là ba cạnh, thông qua đỉnh ‘c’ và ‘h’.

c) Thứ tự duyệt đồ thị theo chiều rộng từ a:

Một thứ tự có thể là: a, b, c, d, f, g, e, h.

Thuật toán duyệt theo chiều rộng (Breadth-First Search, BFS) là một thuật toán duyệt hoặc tìm kiếm trên cây hoặc đồ thị. BFS bắt đầu từ một đỉnh gốc và khám phá các đỉnh lân cận trước khi di chuyển đến các đỉnh xa hơn. Đây là một phương pháp duyệt theo tầng (level-order traversal).

Cài đặt thuật toán BFS

Để cài đặt BFS, chúng ta cần sử dụng một hàng đợi (queue) để theo dõi các đỉnh sẽ được thăm tiếp theo. Hàng đợi đảm bảo rằng các đỉnh được thăm theo thứ tự mà chúng được khám phá.

Dưới đây là các bước cơ bản để cài đặt BFS:

- Khởi tạo hàng đợi: Đẩy đỉnh bắt đầu vào hàng đợi và đánh dấu nó đã được thăm.

- Duyệt đỉnh: Lặp lại quá trình sau cho đến khi hàng đợi rỗng:

+ Lấy đỉnh ở đầu hàng đợi ra.

+ Duyệt tất cả các đỉnh kề của đỉnh này. Nếu một đỉnh kề chưa được thăm, đánh dấu nó đã được thăm và đẩy nó vào hàng đợi.