Mệnh đề sau đúng hay sai?
Giả sử gọi BFS(Adj,s) là chương trình duyệt đồ thị theo chiều rộng bắt đầu từ đỉnh s. Khi đó với mọi đỉnh v thuộc V, hàm BFS(Adj,s) sẽ duyệt qua đỉnh v khi và chỉ khi tồn tại đường đi từ s đến v.
Mệnh đề sau đúng hay sai?
Giả sử gọi BFS(Adj,s) là chương trình duyệt đồ thị theo chiều rộng bắt đầu từ đỉnh s. Khi đó với mọi đỉnh v thuộc V, hàm BFS(Adj,s) sẽ duyệt qua đỉnh v khi và chỉ khi tồn tại đường đi từ s đến v.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Mệnh đề sau là đúng.
- Lý do:
Mệnh đề này có thể được chứng minh tương tự như cách chứng minh tính chất của DFS đối với đường đi trong đồ thị. Cụ thể:
- Chứng minh:
Chúng ta cần chứng minh hai điều sau:
1. Nếu tồn tại đường đi từ đỉnh sss đến đỉnh v, thì quá trình duyệt BFS từ đỉnh sss sẽ duyệt qua đỉnh v.
2. Nếu quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v, thì tồn tại đường đi từ đỉnh sss đến đỉnh v.
- Chứng minh điều 1:
Nếu tồn tại đường đi từ đỉnh s đến đỉnh v:
- Giả sử tồn tại một đường đi từ đỉnh sss đến đỉnhv. Điều này có nghĩa là có một dãy các đỉnh s=v0,v1,v2,…,vk sao cho (vi,vi+1) ∈ E
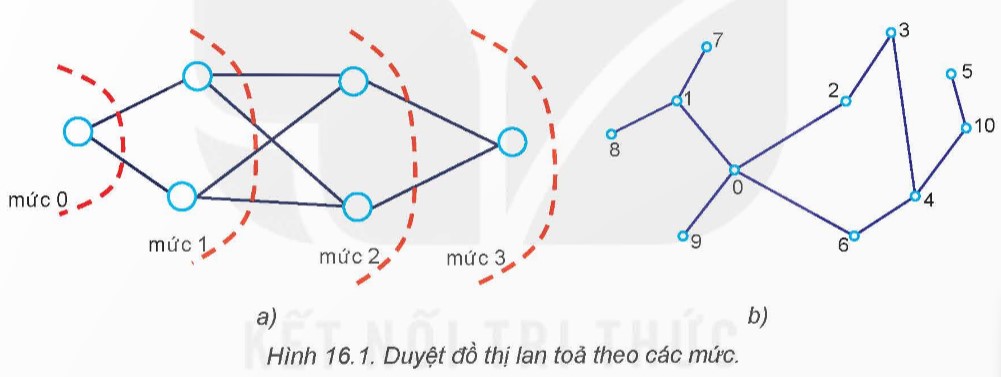
- Khi thực hiện BFS từ đỉnh sss, BFS sẽ thăm tất cả các đỉnh mà nó có thể truy cập được từ sss. BFS duyệt các đỉnh theo từng mức (level) một cách rộng nhất có thể trước khi chuyển sang mức tiếp theo.
- Điều này bao gồm các đỉnh v1,v2,…,vk vì chúng liên tiếp nhau trong đường đi từ s đến v.
- Do đó, nếu tồn tại đường đi từ đỉnh s đến đỉnh v, BFS sẽ chắc chắn thăm đỉnh v trong quá trình duyệt.
- Chứng minh điều 2:
Nếu quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v:
- Giả sử quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v. Điều này có nghĩa là BFS đã bắt đầu từ đỉnh sss và theo các cạnh của đồ thị, nó đã đến đỉnh v.
- BFS duyệt đồ thị bằng cách đi theo các cạnh của đồ thị, nên mỗi bước từ đỉnh hiện tại đến đỉnh tiếp theo trong quá trình duyệt BFS đều là di chuyển qua các cạnh của đồ thị.
- Nếu BFS đã thăm đỉnh v từ đỉnh s, điều đó có nghĩa là có một dãy các đỉnh bắt đầu từ sss và kết thúc tại v sao cho mỗi đỉnh trong dãy này đều có cạnh nối với đỉnh tiếp theo trong dãy.
- Do đó, tồn tại một đường đi từ đỉnh s đến đỉnh v.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
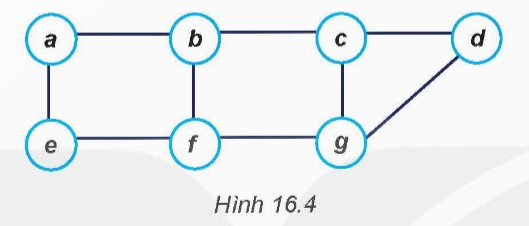
Thứ tự các đỉnh được duyệt khi thực hiện duyệt theo chiều sâu (DFS) và chiều rộng (BFS) bắt đầu từ đỉnh ‘a’:
Duyệt theo chiều sâu (DFS):
- Thứ tự có thể là: a, b, c, d, c, g, b, a, e, f.
Duyệt theo chiều rộng (BFS):
- Thứ tự có thể là: a, b, e, c, f, g, d.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Để kiểm tra xem đồ thị có chu trình hay không, ta có thể sử dụng thuật toán BFS để duyệt đồ thị và kiểm tra xem có đỉnh nào được duyệt lại không. Nếu có đỉnh nào đã được duyệt và nó là đỉnh kề của đỉnh hiện tại, thì đồ thị chứa chu trình.
Dưới đây là một cài đặt Python cho hàm Acycle(G):
from collections import deque
def Acycle(G):
# Hàm kiểm tra có chu trình hay không
def has_cycle(graph, start):
visited = set()
queue = deque([(start, None)]) # Lưu trữ cả cạnh đến đỉnh đang duyệt
while queue:
vertex, parent = queue.popleft()
visited.add(vertex)
for neighbor in graph[vertex]:
if neighbor != parent: # Loại bỏ trường hợp quay lại đỉnh cha
if neighbor in visited:
return True # Đồ thị có chu trình
else:
queue.append((neighbor, vertex)) # Thêm đỉnh kề vào hàng đợi
return False # Đồ thị không có chu trình
# Duyệt qua tất cả các đỉnh của đồ thị
for vertex in G:
if has_cycle(G, vertex):
return False # Nếu có chu trình, trả về False
return True # Nếu không có chu trình, trả về True
# Ví dụ về đồ thị được biểu diễn bằng danh sách kề
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
# Kiểm tra đồ thị có chu trình hay không
print(Acycle(graph)) # False
- Chú ý: Trong hàm Acycle(G), ta duyệt qua tất cả các đỉnh của đồ thị và sử dụng hàm has_cycle(graph, start) để kiểm tra xem có chu trình bắt đầu từ đỉnh đó hay không. Nếu ta tìm thấy bất kỳ chu trình nào, ta trả về False. Nếu không có chu trình nào được tìm thấy, ta trả về True.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập