Cho số phức \(z = a + bi\,\,\left( {a,\,b \in \mathbb{R}} \right)\) thỏa mãn \(\left( {2 + i} \right)\left( {\bar z + 1 - i} \right) - \left( {2 - 3i} \right)\left( {z + i} \right) = 2 + 5i\). Tính \(S = 2a - 3b\).
Quảng cáo
Trả lời:
Ta có \(z = a + bi\,\,\left( {a,\,b \in \mathbb{R}} \right) \Rightarrow \bar z = a - bi\)
Khi đó \(\left( {2 + i} \right)\left( {\bar z + 1 - i} \right) - \left( {2 - 3i} \right)\left( {z + i} \right) = 2 + 5i\)
\( \Leftrightarrow \left( {2 + i} \right)\left( {a - bi + 1 - i} \right) - \left( {2 - 3i} \right)\left( {a + bi + i} \right) = 2 + 2bi\)
\[ \Leftrightarrow \left( {2 + i} \right)\left[ {a + 1 - \left( {b + 1} \right)i} \right] - \left( {2 - 3i} \right)\left[ {a + \left( {b + 1} \right)i} \right] = 2 + 5i\]
\( \Leftrightarrow 2\left( {a + 1} \right) - 2\left( {b + 1} \right)i + \left( {a + 1} \right)i - \left( {b + 1} \right){i^2} - \left[ {2a + 2\left( {b + 1} \right)i - 3ai - 3\left( {b + 1} \right){i^2}} \right] = 2 + 5i\)
\( \Leftrightarrow 2a + 2 - \left( {2b + 2} \right)i + \left( {a + 1} \right)i + b + 1 - 2a - \left( {2b + 2} \right)i + 3ai - 3b - 3 = 2 + 5i\)
\( \Leftrightarrow - 2b + \left( {4a - 4b - 3} \right)i = 2 + 5i \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2b = 2}\\{4a - 4b - 3 = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 1}\end{array}} \right.} \right.\).
Do đó \({\rm{S}} = 2{\rm{a}} - 3\;{\rm{b}} = 2 \cdot 1 - 3 \cdot \left( { - 1} \right) = 5\).
Đáp án: 5.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Các chất tham gia phản ứng tráng gương là có nhóm –CHO, lưu ý fructose có nhóm ketone nhưng trong môi trường \[N{H_3}\] fructose bị chuyển thành glucose nên fructose cũng tham gia phản ứng tráng gương.
→ Các chất tham gia phản ứng tráng gương: glucose, aldehyde acetic, fructose.
Lưu ý: acetylene tham gia phản ứng với \[AgN{O_3}\]nhưng không phải phản ứng tráng gương.
Chọn C.
Lời giải
Ta có: \({\rm{f'}}({\rm{x}}) = 12{{\rm{t}}^2} - 2{{\rm{t}}^3},\,\,{\rm{x}} \in \left[ {0\,;\,\,6} \right]\).
Khảo sát hàm \({\rm{f'}}({\rm{x}})\).
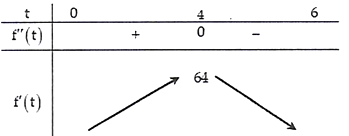
Ta có \({\rm{f''}}(t) = 24t - 6{t^2}\,;\,\,{\rm{f''}}(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 0}\\{t = 4}\end{array}} \right..\)
Vậy tốc độ truyền lớn nhất sẽ lớn nhất vào ngày thứ 4. Đáp án: 4.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.