Câu hỏi:
29/06/2024 2,265
Đọc văn bản sau và trả lời các câu hỏi từ 55 đến 60:
Hệ thống phân loại sinh vật cung cấp thông tin về mức độ tương đối về mối quan hệ giữa các loài. Các nhóm sinh vật được sắp xếp và phân chia vào các bậc khác nhau dựa trên những nguyên tắc nhất định. Căn cứ vào mối quan hệ giữa các nhóm, người ta có thể gộp chúng thành những cấp phân loại cao hơn. Bảng dưới đây cho biết phân loại khoa học của 5 loài.
Phân loại
Lửng Mỹ
Chó sói
Rái cá Châu Âu
Sói xám
Báo hoa mai
Giới
Động vật
(Animalia)
Động vật
(Animalia)
Động vật
(Animalia)
Động vật
(Animalia)
Động vật
(Animalia)
Ngành
Dây sống
(Chordata)
Dây sống
(Chordata)
Dây sống
(Chordata)
Dây sống
(Chordata)
Dây sống
(Chordata)
Lớp
Thú
(Mammalia)
Thú
(Mammalia)
Thú
(Mammalia)
Thú
(Mammalia)
Thú
(Mammalia)
Bộ
Ăn thịt
(Carnivora)
Ăn thịt
(Carnivora)
Ăn thịt
(Carnivora)
Ăn thịt
(Carnivora)
Ăn thịt
(Carnivora)
Họ
Chồn
(Mustelidae)
Chó
(Canidae)
Chồn
(Mustelidae)
Chó
(Canidae)
Mèo
(Felidae)
Chi
Taxidae
Canis
Lutra
Canis
Panthera
Loài
taxus
latrans
lutra
lupis
pardus
Bảng 1. Phân loại khoa học của các loài tương ứng
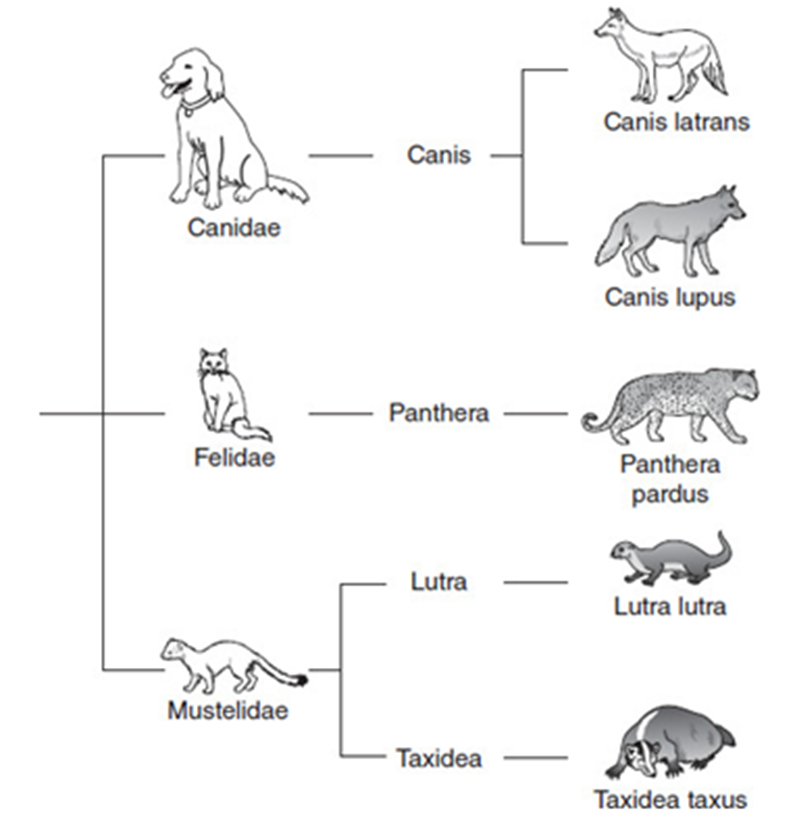
Ngoài ra, các nhà khoa học còn sử dụng cây phát sinh chủng loại để minh họa lịch sử tiến hóa của một nhóm các loài có mối quan hệ mật thiết với nhau, cùng hình thành từ một tổ tiên chung trong quá khứ. Trong một cây phát sinh loại, các loài hiện đang sống được gọi là phân loại còn tồn tại. Điểm mà hai hay nhiều đơn vị phân loại còn tồn tại gặp nhau được gọi là nút. Chiều dài các đường kẻ ngang ước tính khoảng thời gian từ khi đơn vị phân loại trước còn tồn tại cho đến khi phân li thành các loài riêng biệt. Hình dưới đây cho thấy cây phát sinh chủng loại của các loài đã được liệt kê ở bảng 1.
Hình 2. Cây phát sinh thể hiện năm loài của bảng 1
Phân loại lớn nhất trong hệ thống phân loại sinh vật đề cập ở trên là
Đọc văn bản sau và trả lời các câu hỏi từ 55 đến 60:
Hệ thống phân loại sinh vật cung cấp thông tin về mức độ tương đối về mối quan hệ giữa các loài. Các nhóm sinh vật được sắp xếp và phân chia vào các bậc khác nhau dựa trên những nguyên tắc nhất định. Căn cứ vào mối quan hệ giữa các nhóm, người ta có thể gộp chúng thành những cấp phân loại cao hơn. Bảng dưới đây cho biết phân loại khoa học của 5 loài.
|
Phân loại |
Lửng Mỹ |
Chó sói |
Rái cá Châu Âu |
Sói xám |
Báo hoa mai |
|
Giới |
Động vật (Animalia) |
Động vật (Animalia) |
Động vật (Animalia) |
Động vật (Animalia) |
Động vật (Animalia) |
|
Ngành |
Dây sống (Chordata) |
Dây sống (Chordata) |
Dây sống (Chordata) |
Dây sống (Chordata) |
Dây sống (Chordata) |
|
Lớp |
Thú (Mammalia) |
Thú (Mammalia) |
Thú (Mammalia) |
Thú (Mammalia) |
Thú (Mammalia) |
|
Bộ |
Ăn thịt (Carnivora) |
Ăn thịt (Carnivora) |
Ăn thịt (Carnivora) |
Ăn thịt (Carnivora) |
Ăn thịt (Carnivora) |
|
Họ |
Chồn (Mustelidae) |
Chó (Canidae) |
Chồn (Mustelidae) |
Chó (Canidae) |
Mèo (Felidae) |
|
Chi |
Taxidae |
Canis |
Lutra |
Canis |
Panthera |
|
Loài |
taxus |
latrans |
lutra |
lupis |
pardus |
Bảng 1. Phân loại khoa học của các loài tương ứng
Ngoài ra, các nhà khoa học còn sử dụng cây phát sinh chủng loại để minh họa lịch sử tiến hóa của một nhóm các loài có mối quan hệ mật thiết với nhau, cùng hình thành từ một tổ tiên chung trong quá khứ. Trong một cây phát sinh loại, các loài hiện đang sống được gọi là phân loại còn tồn tại. Điểm mà hai hay nhiều đơn vị phân loại còn tồn tại gặp nhau được gọi là nút. Chiều dài các đường kẻ ngang ước tính khoảng thời gian từ khi đơn vị phân loại trước còn tồn tại cho đến khi phân li thành các loài riêng biệt. Hình dưới đây cho thấy cây phát sinh chủng loại của các loài đã được liệt kê ở bảng 1.
Hình 2. Cây phát sinh thể hiện năm loài của bảng 1
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giải thích
Ta thấy trong bảng 1 hệ thống phân loại sắp xếp theo thứ tự từ lớn đến bé là: giới → ngành → lớp → bộ → họ → chi → loài. Chọn B
Câu hỏi cùng đoạn
Câu 2:
Canis latrans là tên khoa học của loài sinh vật nào sau đây?
Lời giải của GV VietJack
Giải thích
Nhìn vào bảng 1, ta thấy tên khoa học chi Canis và tên loài latrans dóng lên thuộc loài chó sói. Chọn A
Câu 3:
Chồn sói có tên khoa học là Gulo gulo thuộc họ Mustelidae. Giả định nào sau đây là hợp lí nhất?
Lời giải của GV VietJack
Giải thích
Theo bảng 1 thì tất cả các loài đều thuộc bộ Ăn thịt (Carnivora). Chồn sói Gulo gulo thuộc họ Mustelidae nên cũng thuộc bộ Ăn thịt (Carnivora). Còn không có thêm dữ kiện nào cho biết nó có họ hàng gần nhất với loài lửng Mỹ hay rái cá châu Âu. Chọn D
Câu 4:
Những phát biểu sau đúng hay sai?
Phát biểu
Đúng
Sai
Trong một cây phát sinh loại, loài đã tuyệt chủng được gọi là đơn vị phân loại còn tồn tại.
Tổ tiên chung gần gũi nhất với cả năm loài kể trên sẽ thuộc bộ Carnivora.
Con người không được sắp xếp vào bất kì hệ thống phân loại sinh vật nào do là động vật bậc cao.
Những phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Trong một cây phát sinh loại, loài đã tuyệt chủng được gọi là đơn vị phân loại còn tồn tại. |
||
|
Tổ tiên chung gần gũi nhất với cả năm loài kể trên sẽ thuộc bộ Carnivora. |
||
|
Con người không được sắp xếp vào bất kì hệ thống phân loại sinh vật nào do là động vật bậc cao. |
Lời giải của GV VietJack
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Trong một cây phát sinh loại, loài đã tuyệt chủng được gọi là đơn vị phân loại còn tồn tại. |
X | |
|
Tổ tiên chung gần gũi nhất với cả năm loài kể trên sẽ thuộc bộ Carnivora. |
X | |
|
Con người không được sắp xếp vào bất kì hệ thống phân loại sinh vật nào do là động vật bậc cao. |
X |
Giải thích
(1) Sai. Theo đoạn thông tin: “...Trong một cây phân loại, các loài hiện đang sống được gọi là phân loại còn tồn tại”.
(2) Đúng. Nhìn vào bảng 1 ta thấy cả 5 loài trên đều mới bắt đầu phân li từ bộ Carnivora thành các họ tương ứng. Có nghĩa là tổ tiên gần gũi nhất với chúng sẽ thuộc đơn vị phân loại Carnivora.
(3) Sai. Con người thuộc giới Động vật, ngành Động vật có xương sống, lớp Động vật có vú, bộ Linh trưởng, họ Người, chi Người. Tên khoa học là Homo sapiens.
Câu 5:
Cho phân loại khoa học của loài linh miêu Á – Âu như sau:
Giới
Ngành
Lớp
Bộ
Họ
Chi
Loài
Động vật
(Animalia)
Dây sống
(Chordata)
Thú
(Mammalia)
Ăn thịt
(Carnivora)
Mèo
(Felidae)
Lynx
lynx
Loài linh miêu này sẽ có họ hàng gần nhất với loài nào trong năm loài được kể trên?
Cho phân loại khoa học của loài linh miêu Á – Âu như sau:
|
Giới |
Ngành |
Lớp |
Bộ |
Họ |
Chi |
Loài |
|
Động vật (Animalia) |
Dây sống (Chordata) |
Thú (Mammalia) |
Ăn thịt (Carnivora) |
Mèo (Felidae) |
Lynx |
lynx |
Loài linh miêu này sẽ có họ hàng gần nhất với loài nào trong năm loài được kể trên?
Lời giải của GV VietJack
Giải thích
Ta thấy loài linh miêu Á – Âu (Lynx lynx) thuộc họ Mèo (Felidae). Trong số năm loài động vật trên thì chỉ có báo là thuộc cùng họ này. Nên giữa hai loài này sẽ có quan hệ họ hàng gần nhau nhất. Chọn B
Câu 6:
Điền từ/cụm từ thích hợp vào chỗ trống dưới đây.
Tên khoa học của loài báo hoa mai là (1) ___________.
Điền từ/cụm từ thích hợp vào chỗ trống dưới đây.
Tên khoa học của loài báo hoa mai là (1) ___________.
Lời giải của GV VietJack
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống dưới đây.
Tên khoa học của loài báo hoa mai là (1) Panthera pardus.
Giải thích
Tên khoa học sẽ được ghép từ tên chi và tên loài, được viết nghiêng, chữ cái đầu tiên của chi sẽ viết hoa, còn lại viết thường. Như vậy, đối chiếu vào bảng 1 ta được tên khoa học của loài báo hoa mai là Panthera pardus.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương trình vận tốc \(v(t) = \int a (t){\rm{d}}t = \int {\left( {{v_0}t + {t^2}} \right)} dt = {v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + C\)
Tại thời điểm \(t = 0 \Rightarrow v(t) = {v_0} \Rightarrow C = {v_0}\)
Vì quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m nên
\(S = 100 = \int\limits_0^3 {v(t)} {\rm{d}}t = \int\limits_0^3 {\left( {{v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + {v_0}} \right)} {\rm{d}}t = 3{v_0} + \frac{9}{2}{v_0} + \frac{{27}}{4} \Rightarrow {v_0} = 12,433\) m/s.
Lời giải
Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \frac{{95{x^2} + 120x}}{4}\), với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần (1) __ 36 __ giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất.
Giải thích
Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\)
\( \Rightarrow \) số công nhân bỏ việc là \(\frac{t}{2}\) nên số công nhân làm việc là \(100 - \frac{t}{2}\) người.
Năng suất của công nhân còn \(120 - \frac{{5t}}{2}\) sản phẩm một giờ.
Số thời gian làm việc một tuần là \(40 + t\) giờ.
Để nhà máy hoạt động được thì \(\left\{ {\begin{array}{*{20}{l}}{40 + t > 0}\\{120 - \frac{{5t}}{2} > 0 \Rightarrow t \in ( - 40;48){\rm{. }}}\\{100 - \frac{t}{2} > 0}\end{array}} \right.\)
Số sản phẩm trong một tuần làm được: \(S = \left( {100 - \frac{t}{2}} \right)\left( {120 - \frac{{5t}}{2}} \right)(40 + t)\).
Số sản phẩm thu được là
\(f(t) = \left( {100 - \frac{t}{2}} \right)\left( {120 - \frac{{5t}}{2}} \right)(40 + t) - \frac{{95{{(40 + t)}^2} + 120(40 + t)}}{4} = \frac{5}{4}{t^3} - \frac{{1135}}{4}{t^2} - 2330t + 440800.\)
\( \Rightarrow {f^\prime }(t) = = \frac{{15}}{4}{t^2} - \frac{{1135}}{2}t - 2330.\)
\({f^\prime }(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 4\,\,\,\,\,\,\,\,\,\,\,}\\{t = \frac{{466}}{3}\,\,(\;{\rm{L}})}\end{array}} \right.\)
Ta có BBT như sau
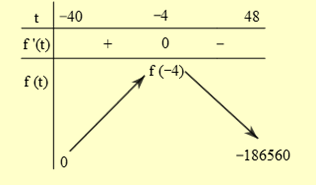
Vậy số lượng sản phẩm thu được mỗi tuần lớn nhất khi x = 36.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)